Բովանդակություն

Դեռևս մ.թ.ա. շատ մեծ փիլիսոփաներ, շրջապատում նկատվող երևույթները բացատրելու համար նյութերի և մարմինների կառուցվածքի մասին անում էին հետևյալ ենթադրությունները`

1. Ցանկացած նյութ կամ մարմին բաղկացած է մեզ համար անտեսանելի, փոքր մասնիկներից:
2. Այդ մասնիկները գտնվում են անընդհատ քաոսային շարժման մեջ:
3. Մասնիկները փոխազդում են միմյանց հետ, այսինքն կախված իրենց դիրքից և տեսակից միմյանց ձգում կամ վանում են:
4. Առանց բացառության բոլոր մարմինների հատկությունները որոշվում են այդ մարմինը կազմող մասնիկների հատկություններով:

Գիտության զարգացման ընթացքում այս ենթադրությունները ստացան փորձնական հիմնավորումներ և ներկայումս ընդունվում են որպես մոլեկուլային-կինետիկ տեսության հիմնական դրույթներ: Ընդունվում են, որ վերընշված մասնիկներն են նյութի մոլեկուլները, ատոմները և մոլեկուլը կազմող այլ տարրական մասնիկները: Այժմ այս դրույթները առանց կասկածի տակ դրվելու օգտագործվում են զանազան ֆիզիկական և քիմիական երևույթներ բացատրելու, նրանց ընթացքը կանխատեսելու և նրանց ի շահ մարդուն օգտագործելու համար: Հաջորդ դասերում մենք կբերենք մի քանի փորձեր, որոնցով կփորձենք հիմնավորել նշված դրույթները:

Բրոունյան շարժում

Մարմինների մեջ մոլեկուլների առկայության և նրանց քաոսային շարժման փորձնական ապացույցը կարելի է ստանալ վերլուծելով անգլիացի գիտնական Բրոունի 1827 թվականին հայտնաբերած երևույթը: Հաճախ, երբ հեղուկի հետ խառնում ենք նրա մեջ դժվար լուծվող մեկ այլ հեղուկ կամ նյութ, ապա հեղուկի մեջ առաջանում է այդ չլուծված նյութի կամ հեղուկի մանրագույն հատկիների կախույթ, նման կախույթը կոչվում է էմուլսիա: Եթե մանրադիտակով դիտենք այդ էմուլսիան` կնկատենք, որ այդ էմուլսիայում առկա հատիկները գտնվում են անընդհատ քաոսային շարժման մեջ, և այդ շարժումն է, որ կոչվում է բրոունյան շարժում:

Բրոունյան շարժումը դիտելու համար կարելի է, օրինակ, ջրի հետ խառնել փոքր քանակությամբ սև տուշ և մանրադիտակի տակ դիտել տուշի մանր հատիկները ջրի կաթիլի մեջ: Հեղուկների մեջ նկատվող բրոունյան շարժումն այնքան ավելի աշխույժ է լինում, որքան հեղուկը քիչ մածուցիկ է: Դիտարկումները ցույց են տալիս, որ բրոունյան շարժումը երբեք չի դադարում: Նա սերտ կապված է հեղուկի ջերմային վիճակի հետ: Ջերմաստիճանի բարցրացման զուգընթաց բրոունյան շարժման ինտենսիվությունն աճում է:

Սակայն ի՞նչն է էմուլսիայում այդ հատիկների քաոսային շարժման պատճառը: Այն կարելի է բացատրել, եթե ընդունենք, որ իրոք շարժվող հատիկներին շրջապատող հեղուկը բաղկացած է առանձին և անընդհատ շարժման մեջ գտնվող մոլեկուլներից:

Ուղղակի այդ մոլեկուլները շատ փոքր են և մանրադիտակով չեն երևում: Ըստ երևույթին իրենց շարժման ժամանակ մոլեկուլները դիպչում են էմուլսիայի հատիկներին, տեղից շարժում նրանց և այդպիսով, անուղղակի կերպով, հանդես բերում իրենց առկայությունը: Պարզ է, որ հեղուկի շարժվող մոլեկուլները հատիկը հրում են միաժամանակ ամեն կողմից, բայց քանի որ մոլեկուլների շարժումը միանգամայն քաոսային բնույթ է կրում, ապա ակներև է, որ մասնիկը շարժումը միանգամայն քաոսային բնույթ է կրում, ապա ակներև է, որ մասնիկը երբեմն մեկ կողմից կարող է ստանալ ավելի մեծ թվով հարվածներ, երբեմն մյուս կողմից, և այդ ստիպում է նրան շարժվել զիգզագաձև հետագծով: Ըստ մեզ հեղուկի մեջ տեղավորված սովորական, այսինքն` բավական մեծ չափեր ունեցող մարմինը նույնպես հարվածների է ենթարկվում հեղուկի շարժվող մոլեկուլների կողմից, բայց այս դեպքում մարմնի չափերի մեծությունը բերում է հարվածների թվի մեծացմանը և տարբեր կողմից տրվող հարվածների տարբերությունը արդեն խիստ փոքր է լինում հարվածների ընդհանուր քանակի նկատմամբ և այդպիսի աննշան տարբերությունը չի կարող շարժման մեջ դնել հեղուկում գտնվող մեծ մարմինը: Այդպիսի մարմինը ջրի մեջ մնում է անշարժ: Բրոունյան շարժման ժամանակ մեր դիտած մանրադիտակային հատիկների դեպքում նրանց կրած հարվածների թիվն արդեն այնքան մեծ չէ, ուստի այդ հարվածները միշտ մեկ կամ մյուս կողմից գերակշռում են, և փոքր հատիկն այս ու այն կողմ է շարժվում: Պետք է լավ հասկանալ, որ բրոունյան շարժման ժամանակ մեր դիտած հատիկներից յուրաքանչյուրը միլիոնավոր մոլեկուլներ է պարունակում, ուստի նրա կատարած անկանոն շարժումը, իսկապես ասած, մոլեկուլային շարժում չէ: Առանձին մոլեկուլի հարվածները մենք նկատել չենք կարող, այլ տեսնում ենք միայն մոլեկուլների հարվածների պատահական գերակշռությունը մի որևէ ուղղությամբ: Իհարկե վերը նշվածը ուղղակիորեն չի հաստատում նյութում մոլեկուլների առկայության և նրանց շարժման փաստը, սակայն մեր ենթադրությունը նրանց առկայության մասին բացատրեց փաստացի նկատված բրոունյան շարժումը և դրանով իսկ խիստ հավանական դարցրեց այն:

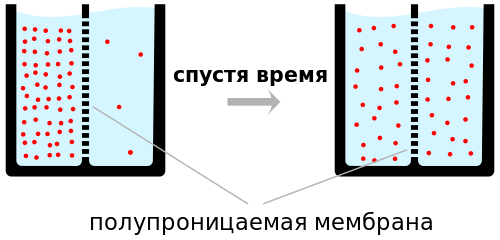
Դիֆուզիա

Այժմ նկարագրենք մեկ այլ երևույթ, որի բացատրությունը ևս մեկ անգամ հիմնավորում է նյութի մոլեկուլային կառուցքի փաստը: Եթե պղնձարջասպի լուծույթով կիսով չափ լցված անոթի մեջ՝ լուծույթի վրա զգուշությամբ մաքուր ջուր լցնենք, ապա սկզբում կստացվի որոշակի նկատվող AB բաժանման մակերևույթը՝ անգույն ջրի և կապույտ լուծույթի միջև: Սակայն որոշ ժամանակ անցնելուց հետո կարելի է նկատել, թե ինչպես ջուրն աստիճանաբար սկսում է կապտել, բաժանման մակերևույթը դադարում է խիստ որոշակի լինելուց, իսկ երկար ժամանակ անցնելուց հետո բոլորովին անհետանում է: Տվյալ փորձի մեջ մենք հանդիպում ենք մի նոր ֆիզիկական երևույթի, որ կոչվում է դիֆուզիա: Դիֆուզիան զանազան մարմինների փոխադարձ ներթափանցման երևույթն է, երբ այդ մարմինները հպման մեջ են դրվում իրար հետ: Դիֆուզիան առանձնապես հեշտ է նկատել գազերի մեջ: Կշեռքի վրա հավասարակշռված բաժակը լցնում ենք եթերի ծանր գոլորշիներով: Կշեռքի այն նժարը, որի վրա գտնվում է եթերի գոլորշիներով լցված բաժակը, ծանր է կշռում: Մի որոշ ժամանակից հետո նկատում ենք, որ կշեռքը հավասարակշռվում է, իսկ սենյակում եթերի հոտ է զգացվում: Այդ նշանակում է, որ չնայած եթերի գոլորշիներն ավելի ծանր են, քան օդը, այնուամենայնիվ նրանք բաժակից թափանցել են սենյակի մեջ: Դիֆուզիայի երևույթը նկատվում է ոչ միայն հեղուկների և գազերի, այլև պինդ մարմինների մեջ: Մի փորձի ժամանակ կապարի և ոսկու լավ հղկված թիթեղները տեղավորել էին իրար վրա և նրանց վրա դրել մեծ ծանրություն: Սենյակի սովորական ջերմաստիճանում (մոտ 20°C) 5 տարի անցնելուց հետո ոսկին և կապարը ներաճել էին՝ փոխադարձաբար ներթափանցելով իրար մեջ 1սմ-ով: Ստացվել էր կապարի և ոսկու համասեռ համաձուլվածքի մի շերտ, թեպետ, իհարկե, 20°C ջերմաստիճանում այդ մետաղների հալման մասին խոսք լինել անգամ չէր կարող: Այստեղ նկարագրված փորձերի արդյունքները հեշտությամբ բացատրվում են մոլեկուլային-կինետիկ տեսության օգնությամբ: Եվ իրոք, եթե ընդունենք որ իրար հետ հպման մեջ գտնվող մարմինները բաղկացած են առանձին, անկանոն կերպով շարժվող մոլեկուլներից, ապա բնական է, որ այդ մոլեկուլները իրենց շարժման ընթացքում կարող են անցնել մարմինների հպման սահմանից, իսկ այդ երևույթը հենց դիֆուզիան է: Դիֆուզիայի վերաբերյալ փորձերից կարելի է նույնպես եզրակացնել, որ մարմինների մոլեկուլների միջև կա ազատ տարածություն, որտեղ կարող են ներթափանցել ուրիշ մոլեկուլներ: Եթե դիֆուզիայի երևույթը տեղի է ունենում, երբ տարբեր նյութեր հպման մեջ են դրվում իրար հետ, ապա նա տեղի կունենա նաև միևնույն գազի կամ հեղուկի մեջ:

Այդ է պատճառը, որ գազի խտությունն իր ամբողջ ծավալում հավասար է դառնում:

Ջերմաստիճանի բարցրացման հետևանքով դիֆուզիայի պրոցեսն արագանում է: Սա կարելի է բացատրել է նրանով, որ ջերմաստիճանի բարցրացման ժամանակ մեծանում է մոլեկուլների անկանոն շարժումների արագությունը:

Մոլեկուլների փոխազդեցության ուժերը

Ըստ առաջին պարագրաֆում բերված մոլեկուլային-կինետիկ տեսության հիմնական դրույթների նյութական մարմինները կազմող մասնկիները` մոլեկուլներն ու ատոմները գտնվում են միմյանց հետ փոխազդեցության մեջ, այսինքն նրանց միջև գործում է միմյանց ձգող և վանող ուժեր: Այդ միջատոմային կամ միջմոլեկուլային փոխազդեցության ուժերի առկայության ապացույցը կարելի է ստանալ փորձնական ճանապարհով: Օրինակ փորձենք կոտրել հաստ փայտը: Մենք նկատում ենք, որ դրա համար անհրաժեշտ է մեծ ուժ կիրառել: Սա կարելի է բացատրել նրանով, որ փայտը կազմված է մոլեկուլներից որոնց միջև կան ձգողական ուժեր:Իրոք որ հետագայում մենք կապացուցենք որ ցանկացաց նյութական մարմիններ ձգում են միմյանց: Օրինակ տիեզարքում արևը ձգում է մոլորակներին, այդպիսի ձգողական ուժերը կոչվում են գրավիտացիոն ուժեր և այդ ուժերը կտրուկ մեծանում են երբ փողազդող մարմինների միջև հեռավորությունը փոքրանում է:Իսկ մեր դիտարկախ մոլեկուլները նույնպես նյութական մարմիններ են, ճիշտ է շատ փոքր չափերի բայց միևնույն ժամանակ գտնվում են միմիանցից շատ փոքր հեռավորության վրա, այսինքն նրանց միջև առաջանում է միմիանց ձգող գրավիտացիոն ուժեր:Որոնք էլ փայտի մոլեկուլներին կապում են միմիանց և տալիս են փայտին ամրություն:Իսկ մեր գործադրած ուժը փայտի վրա հակազդում է այդ ձգող ուժերին, մոլեկուլներին հեռացնում միմյանցից` կոտրում փայտը: Եթե փայտի մոլեկուլների միջև չլինեին ձգողության ուժեր, ապա այդ փայտը չէր ունենա ամրություն: Քանի որ (ըստ նախորդ դասերում բերված ապացույցների) ցանկացած մարմնի մոլեկուլներ գտնվում են անընդհատ քաոսային շարժման մեջ, շարժման մեջ կլինեին նաև փայտի մոլեկուլները: Նման դեպքում փայտը չէր լինի ամբողջական մարմին, կնմանվեր գազի: Այսպիսով մոլեկուլների ձգողության ուժերի շնորհիվ է միայն, որ մոլեկուլները պահվում են իրար մոտ և կազմում հեղուկ ու պինդ մարմիններ: Սակայն միմիայն ձգողության ուժերը չեն կարող ապահովել ատոմներից և մոլեկուլներից կազմված կայուն մարմիններ: Եթե լինեին միայն ձգողական ուժեր, ապա մարմնի մոլեկուլները կմխրճվեին միմյանց մեջ: Ստորև մենք ցույց կտանք, որ շատ փոքր հեռավորությունների վրա մոլեկուլների միջև կան նաև վանողական ուժեր: Այս պնդումը բացատրվում է մոլեկուլի կառուցվածքի մասին ներկայումս ֆիզիկայում ընդունված հետևյալ պնդումով: Մոլեկուլը բարդ համակարգ է, որը բաղկացած է դրական լիցք ունեցող միջուկից և նրա շուրջը պտտվող բացասական լիցք ունեցող էլեկտրոններից(այդ պտտվող էլեկտրոնների բազմությունը անվանում են Էլեկտրոնային թաղանթ): Միջուկի դրական լիցքի և էլեկտրոնային թաղանթի բացասական լիցքի արժեքները միմյանց հավասար են, այսինքն մոլեկուլը որպես մի ամբողջոթյուն էլեկտրաչեզոք է:

Երբ մենք փորձում ենք սեղմել նյութական մարմինը, ապա բնական է, որ նրա մոլոկուլները փորձում են միմյանց մոտենալ: Այսինքն մոտենում են միմիանց նաև երկու հարևան մոլեկուլների էլեկտրոնային թաղանթները: Ֆիզիկայի էլեկտրականություն բաժնում ապացուցվում է, որ համանուն լիցքերը միմյանց վանում են, ընդ որում վանողական ուժը հակադարձ համեմատական է լիցքերի միջև եղած հեռավորության քառակուսուն: Այսինքն մոտ գտնվող լիցքերի համար վանող ուժը մեծ է, իսկ լիցքերը միմյանցից հեռացնելիս այդ ուժերը արագորեն թուլանում են: Այնպես որ երբ մարմինը սեղմելիս մոլեկուլները մոտենում են միմյանց, միմյանց են մոտենում նաև նրանց բացասական լիցքավորված էլեկտրոնային թաղանթները: Առաջանում են վանողական ուժեր այդ թաղանթների միջև, քանի որ թաղանթները մոլեկուլների բաղադրիչ մասերն են, ապա առաջանում են վանողական ուժեր նաև մոլեկուլների միջև: Հեռավորության փոքրացման զուգընթաց մոլեկուլների միջև ձգողության ուժն սկզբում աճում է: Բայց հեռավորության հետագա փոքրացման զուգընթաց սկսում է ի հայտ գալ վերը նկարագրված վանողության ուժը: Վերջինս շատ արագ աճում է, երբ ատոմների էլեկտրոնային թաղանթներն սկսում են մխրճվել միմյանց մեջ:Կոշտ մարմնում երկու հարևան մոլեկուլների միջև հաստատվում է այնպիսի հեռավորություն, որի դեպքում այդ հարևան մոլեկուլների միջև գործող վանողական և ձգողական ուժերը միմյանց հավասարակշռում են: Մարմնի երկրաչափական չափերը, որոնք պայմանավորված են միջմոլեկուլային հեռավորություններով, ստանում են կայուն արժեքներ:Երբ մենք փորձում ենք արտաքին ազդեցությամբ ձգելով կամ սեղմելով մարմինը փոխել նրա արտաքին չափերը (առաջացնել մարմնի դեֆորմացիա)ապա փոփոխվում է նաև մոլեկուլների միջև գործող վանող և ձգող ուժերի հավասարակշռությունը:Երբ մենք վերացնում ենք արտաքին ազդող ուժերը ապա նյութի մոլեկուլները փորձում են նորից վերականգնել խախտված հավասարակշռությունը, այսինքն վերականգնել մարմնի սկզբնական չափերը:Պինդ մարմինների մոտ նկատվող այս երևույթը և նրանց այս հատկությունը անվանում են մարմնի առաձգականություն:Մարմնի ներսում գործող ուժը, որը մարմնին վերադարձնում է սկզբնական դիրքին կոչվում է առաձգականության ուժ,այն հավասար է մարմնի դեֆորմացիայի ուժին: Անգլիացի ֆիզիկոս Հուկը հայտնաբերել է որ դեֆորմացիայի չափը և դեֆորմացիայի ուժի միջև կա գծային համեմատականություն, այսինքն դեֆորմացիայի ուժը մեծացնելիս նրան համեմատական չափով մեծանում է դեֆորմացիայի չափը:

Գազային, Հեղուկ և Պինդ Մարմինների կառուցվածքը

Մեզ թվում է նախորդ դասերի նյութերը մեզ բավարար չափով հիմք տվեցին, որ մենք ընդունենք մոլեկուլային-կինետիկ տեսության հիմնական դրույթները, սակայն այդ քննարկումները ինքնանպատակ չէին: Նշված դրույթները մեզ թույլ կտան բացատրել մեզ շրջապատող շատ երևույթներ, մասնավորապես կարելի է բացատրել ինչու է նյութը գտնվում գազային, պինդ և հեղուկ վիճակներում:

Գազեր, Երկրի մթնոլորտ: Մարդն իր կենսագործունեության ընթացքում շփվում է Գազի, գազային բնույթի օբյեկտների հետ: Օրինակ Ամպերը, գոլորշու քուլաները, մթնոլորտը որում մենք գոյատևում ենք, բուրումնավետ գազերը, որանք մենք շնչում ենք: Այս օբյեկտները չունեն որոշակի ձև և ծավալ, կարող են անսահման ընդարձակվել, ինչպես նաև սեղմվել(օրինակ` Մխոցով): Գազային օբյեկտների այս հատկությունները փորձենք բացատրել նյութի վերն շարադրված մոլեկուլային-կինետիկ տեսության հիմնական դրույթներով: Ելնելով այդ դրույթներից ընդունենք, որ գազային օբյեկտները նույնպես բաղկացած են մոլեկուլներից և ատոմներից, բայց նրանցում ատոմների կամ մոլեկուլների միջև եղած հեռավորությունները միջին հաշվով շատ անգամ ավելի մեծ են, քան իրենց` մոլեկուլների չափերը: Սա է պատճառը, որ գազերը հեշտությամբ սեղմվում են: Գազերը հեշտությամբ սեղմվում են, քանի որ գազի սեղմման ժամանակ փոքրանում է միայն մոլեկուլների միջև եղած միջին հեռավորությունը, բայց մոլեկուլներն իրար չեն <<ճզմում>>: Մենք արդեն հիմնավորել ենք, որ նյութի մոլեկուլները գտնվում են անընդատ շարժման մեջ: Գազերի դեպքում մոլեկուլների շարժման արագությունը խիստ մեծ է: Այնպես որ գազի մոլեկուլները հսկայական արագություններով (հարյուրավոր մետր-վայրկյան) շարժվում են տարածության մեջ: Բախվելով իրար` բիլիարդի գնդերի նման նրանք միմյանցից ետ են թռչում տարբեր ուղղություններով: Գազի մոլեկուլների ձգողության թույլ ուժերը նրանց իրար մոտ պահել չեն կարող: Այդ է պատճառը որ գազերը կարող են անսահմանորեն ընդարձակվել և նրանք չեն պահպանում ո'չ ձևը, ո'չ ծավալը: Օրինակ որպես Գազային բնույթ ուեցող օբյեկտ, որի վրա կտարածվեն մեր գազի մասին կատարած մտահանգումները, դիտարկենք երկրի մթնոլորտը: Այն իրենից ներկայացնում է մի քանի հարյուր կիլոմետրի հասնող անընդատ նվազող խտությամբ գազի մոլեկուլների շերտ: Օդի մոլեկուլները գտնվում են երկրի ձգողության ազդեցության տակ, այսինքն նրանք անընդատ սեղմվում են դեպի երկրի մակերևույթը: Օդի նման սեղման պատճառով էլ նրա խտությունը երկրի մակերևույթի մոտ շատ ավելի մեծ է քան նրա վերին շերտերում: Միայն մոլեկուլների անընդհատ շարժումով կարելի է բացատրել այն իրողությունը, որ չնայած իրենց կշռին, մթնոլորտում պարունակած գազերը անմիջապես չեն գտնվում Երկրի մակերևույթի վրա: Գազերի մոլեկուլների նման բաշխումը մթնոլորտի մեջ հետևանք է մի կողմից ձգողական ուժի ազդեցությանը, որ ձգում է մոլեկուլները դեպի Երկիրը, և մյուս կողմից օդի մոլեկուլների շարժմանը, որ ցրիվ է տալիս մոլեկուլներն ամեն ուղությամբ: Օդի մթնոլորտի խտության բաշխումը պարզելու համար, մարդիկ օգտագործել են տարբեր բարձրությունների վրա թռչող սարքեր` ինքնաթիռներ, օդապարիկներ և արհեստական արբանյակներ: Օրինակ վերջինիս օգնությամբ Երկրի մթնոլորտի հետքերը հայտնաբերված են Երկրի մակերևույթից 1500 կմ և ավելի բարձրության վրա: Ներկայումս գիտության մեջ ընդունված է Երկրի մթնոլորտի շերտերի հետյալ դասակարգումը: 1. Արոպոսֆերա - Շերտի հաստությունը Երկրի մակերևույթից 10-16 կմ: Պարունակում է մթնոլորտի մասսայի 79%-ը և ավելին 2. Ստրոտոսֆերա - Շերտի հաստությունը Երկրի մակերևույթի 10-16 կմ-ից միջև 80-90կմ: Պարունակում է մթնոլորտի ամբողջ մասսային մոտ 20%-ը: 3. Իոնոսֆերա - Սկսում է Երկրի մակերևույթի 80-90 կմ-ից միջև 1500 կմ և ավելին: Պարունակում է մթնոլորտի մասսային 0,5%-ից էլ պակաս: Հեղուկներ:Հեղուկները էապես տարբերվում են գազերից:Նկատում ենք որ 1)ունեն շատ ավելի մեծ տեսակարար կշիռ, 2)նրանք ընդունում են այն անոթի ձևը որի մեջ լցված են, 3)նրանք կարող են հոսել,որի ժամանակ չի խաղտվում նրանց ամբողջականությունը (օրինակ գետերը և առուները), 4)սովորաբար անսեղմելի են: այժմ փորձենք բացատրել այս հատկությունները հիմք ընդունելով այն դրույթները որ հեղուկները ևս բաղկացաց են ատոմներից և մոլեկուլներից, որոնք գտնվում են քաոսային շարժման մեջ:

1)Մեծ տեսակարար կշռի հիմնավորումՀեղուկի տեսակարար կշռի մեծ լինելը (ի տարբերություն գազերի) կարելի է բացատրել նրանով,որ հեղուկներում մոլեկուլները գրեթե իրար կիպ են դասավորված:Դրանով է բացատրվում հեղուկի տեսակարար կշռի մեծ լինելը: 2)Ընդունած ձևի հիմնավորումՄոլեկուլների իրար մոտ լինելու պատճառով մոլեկուլը հեղուկում իրեն պահում է ոչ այնպես, ինչպես գազում:Հեղուկի յուրաքանչյուր մոլեկուլ, բոլոր կողմերից սեղմված լինելով մյուս մոլեկուլներով, կարծես թե գտնվում է <<վանդակում>>,իսկ նրա շարժունակությունը արտահայտվում է իր հավասարակշռության կետի շուրջը տատանմնան տեսքով:Ժամանակակից ֆիզիկայի մեթոդներով հաշվարկվել է որ ջրի մոլեկուլների տատանվելու պարբերությունը(այն ժամանակամիջոցը որի ընթացքում կատարվում է 1 տատանում) սենյակային ջերմաստիճանում միջին հաշվով հավասար է 10^-12-10^-13 վ:Նման տատանումների ընթացքում նյութի մոլեկուլը բախվում է իր հարևան մոլեկուլներին և որոշակի չափով հրում նրանց,պինդ նյութից կազմված անոթի պատերի մոլեկուլները արդեն նման հրումներից չեն տեղաշարժվում:Այսպիսով հեղուկի մոլեկուլների հրումների արդյունքում էլ հեղուկի մոլեկուլների բազմությունը(ինքը հեղուկը) ընդունում է այն անոթի տեսքը որում նա լցված է: 3)Հոսունության հիմնավորումՄոլեկուլների տատանումների ժամանակ, երբեմն հեղուկի մոլեկուլները դուրս են գալիս իրենց <<վանդակներից>> և չհանդիպելով հեղուկատար անոթի պատերով պայմանավորված արգելքներին հոսում են որոշակի ուղղությամբ:Քանի որ մոլեկուլներն ունեն կշիռ, նրանք ձգվում են երկրի կողմից: Սովորաբար մոլեկուլների այդ հոսքը ընդանում է բարձր դիրքից դեպի ցածր ուղղությամբ:Նման ձևով է բացատրվում գետերի, առուրերի ջրի հոսքը բարձր դիրքից դեպի ցածր դիրք: 4)Անսեղմելիության հիմնավորումՀեղուկի մոլեկուլները անմիջապես իրար մոտ են գտնվում: Ուստի հեղուկի ծավալը փոքր-ինչ փոփոխելու փորձի դեպքում անգամ սկսվում են դեֆորմացվել հենց իրենք` մոլեկուլները: Իսկ դրա համար արդեն շատ մեծ ուժեր են պետք: Դրանով էլ հենց բացատրվում է հեղուկների փոքր սեղմելիությունը:

Պինդ մարմիններ: Ի տարբերություն հեղուկների,պինդ մարմինները պահպանում են ոչ միայն ծավալը, այլև ձևը: Փորձենք բացատրել պինդ մարմնի այս հատկությությունը կինետիկ մոլեկուկյար տեսության դրույթներով:Ըստ երևույթի պինդ մարմնի ատոմները կամ մոլեկուլները ունեն տատանման ավելի փոքր տիրույթ և տատանվում են հավասարակշռության որոշակի դիրքերի շուրջը: Ճիշտ է, երբեմն մոլեկուլները փոխում են հավասարակշռության դիրքը, բայց դա տեղի է ունենում շատ հազվադեպ: Պինդ մարմնի հատկությունները հասկանալու համար կարելի է հեղուկը համեմատել այն ամբոխի հետ, որի առանձին անդամներ անհանգիստ հրմշտվում են տեղում, իսկ պինդ մարմինը նման է զորասյան, որի անդամները իրենց տեղերում թեպետ <<զգաստ>> չեն կանգնած (ջերմային շարժման հետևանքով),բայց միմյանց միջև պահպանում են միջին հաշվով որոշակի միջակայքեր:Այս դիրքի կայունության հաշվին էլ զորասյանը չի փոխում իր ձևը, և նրա նման պինդ մարմինն էլ չի փոխում իր ձևը:Որոշ պինդ մարմինների մոտ (օրինակ մետաղների), եթե միացնենք տատանման հավասարակշռության կենտրոնները, ապա կստացվի կանոնավոր տարածական պատկերներ:Որոնցից յուրաքանքյուրը նման է որևէ կանոնավոր բյուրեղի պատկերի, այդ պատճառով տարածական պատկերը անվանում են բյուրեղային ցանց:

Նյութի մոլեկուլների պարամետրերի գնահատում

Նյութի մոլեկուլների պարամետրերի որոշումը անուղղակի եղանակով

Մենք նախորդ գլխում համոզվեցինք որ իրոք մարմինները բաղկացած են փոխազդեցության մեջ գտնվող մանրագույն մասնիկներից` մոլեկուլներից:Այժմ փորձենք որոշել այդ մոլեկուլների պարամետրերը` մասսան (m), չափերը (տրամագիծը-d), նրանց շարժման արագություն(v): Սակայն մոլեկուլների չափազանց փոքր լինելը մեզ թույլ չի տալիս որոշել այդ պարամետրերը ուղղակի չափումներով: Մենք փորձենք այն որոշել անուղղակի չափման ճանապարհով` որն է այդ ճանապարհը: Դիտարկման ենթարկենք ոչ թե մի մոլեկուլը այլ այդ մոլեկուլների հսկայական բազմությունից կազմված համակարգը: Որպես այսպիսի դիտարկման օբյեկտ մենք կվերցնենք գազը: Նման գազային օբյեկտի համար արդեն կարելի է չափել նրա պարամետրերը` գազի ճնշումը ջերմաստիճանը ծավալը կշիռը: Եթե մենք ունենանք սրանց կախվածությունը մոլեկուլի պարամետրերից ապա պարզ է որ մաթեմաթիկական հաշվարկներով կարող ենք որոշել նրանց պատճառ հանդիսացող մոլեկուլի պարամետրերը (m, d, v): Իսկ ինչու ենք որպես դիտարկման օբյեկտ վերցնում գազը: Բանը նրանում է որ ինչպես արդեն նշել ենք գազում մոլեկուլները գտնվում են միմիանցից չափազանց հեռու, նրանց հեռավորությունը շատ ավելի մեծ է քան մոլեկուլի տրամագիծը:Նման պայմաններում արդեն առհամարելի են դառնում գազի մոլեկուլների միջև եղած փոխազդեցության ուժերը: Հետևաբար և առհամարելի են դառնում այդ ուժերի ազդեցությունը գազի պարամետրերի վրա: Արդյունքում գազի պարամետրերի կախվածության արտահայտությունները իր մոլեկուլների պարամետրերից ստացվում է ավելի պարզ, Որը հեշտացնում է անուղղակի ճանապարհով մոլեկուլների պարամետրերի հաշվարկման գործընթացը: Բայց կան արդյոք կախվածություններ p,v,t-ի և m,d,v-ի միջև: Վերհիշենք դիֆուզիայի երևույթը: Մենք արդեն փորձնական ճանապարհով նկատել ենք որ դիֆուզիայի խորությունը ուղակիորեն կախված էր հպված մարմինների ջերմաստիճաններից: Իսկ դիֆուզիան բացատրվում էր այն փաստով որ մոլեկուլները գտնվում էին քաոսային շարժման մեջ, և նյութերի միմյանց մեջ ներթափացման խորությունը բնական է կախված այդ մոլեկուլների արագությունից: կարող ենք հետևություն անել որ տաքացնելով մարմինները` մեծացնելով t-ն փաստորեն մեծանում է մոլեկուլների արագությունը, այդ իսկ պատճառով մեծանում է մարմինների իրար մեջ ներթափացման խորությունը: Այսինքն մարմնի ջերմաստիճանը կախված է այն կազմող մոլեկուլի արագությունից: Հեշտ է բացատրել նաև որ գազի ծավալը նույնպես կախված է մոլեկուլի արագությունից: Քանի որ գազի մոլեկուլների մեծ արագությունների ժամանակ նրանք ունենում են ցրվելու ավելի մեծ հնարավորություն` ավելի մեծ ծավալ գրավելու հնարավորություն: Խոսենք գազի ճնշման մասին:Ճնշման պատճառը դա գազի մոլեկուլների բախումն է անոթի պատերին: Բնական է որ այդ ճնշումը կլինի այնքան մեծ որքան մեծ է պատին բախվող մոլեկուլների մասսան և արագությունը: Ուրեմն ճնշումը ևս կախված է մոլեկուլի պարամետրերից: Այսպիսով մենք ցույց տվեցինք մոլեկուլների պարամետրերի անուղակի չափման հնարավորությունը ելնելով նրանցով կազմված մարմնի` գազի պարամետրերից: Սակայն այս չափումները իրականացնելու համար պետք է ունենալ վերընշված կախվածությունների ճշգրիտ անալիտիկ արտահայտությունները, ոչ թե խոսքային(որակական)այլ նրանց մաթեմաթիկական բանաձևերը: Այդ անալիտիկ արտահայտությունները մենք կստանանք այս գլխի հաջորդ կետերում:

Ջերմաստիճան:Ջերմաչափ

Մարմնի մոլեկուլների պարամետրերի չափման գործընթացը իրականացնելու համար առաջնահերթ է նրա ջերմաստիճանի որոշումը և ընդհանրապես ջերմային երևույթների մասին ուսմունքի մեջ կենտրոնական տեղ է գրավում ջերմաստիճանի հասկացությունը: Իսկ ինչ բան է այն: Մենք բոլորս լավ գիտենք սառը և տաք մարմինների տարբերությունը: Շոշափելով մենք կարող ենք որոշել, թե որ մարմինն է ավելի ուժեղ տաքացրած, և ասում ենք, որ այդ մարմինն ունի առավել բարձր ջերմաստիճան: Այսպիսով ջերմաստիճանը բնութագրում է մարմնի տաքացածության աստիճանը (սառը, տաք, այրող):Սակայն միշտ չէ որ հնարավոր է ջերմաստիճանը որոշելիս հենվել մեր զգայարանների վրա: Ջերմասճանն կարող է լինել շատ բարձր կամ ցածր, և մեր զգայարանները կարող են դրանք չընկալել: Նման ձևով ջերմաստիճանը մեր զգայարաններով կարող ենք գնահատել որակապես,այսինքն ջերմաստիճանը որոշում ենք ընդհատ ձևով, մոտավորապես, իսկ բառերով արտահայտված բնորոշումներն էլ իրենց քանակով սահմանափակ են (մարմինը շատ սառն է,սառն է, գոլ է, տաք է և այլն), իսկ իրականում ջերմաստիճանն անընդհատ մեծություն է ունի չափ որը պետք է արտահայտվի թվով: Մարմնի 5երմաստիճանի թվային արժեքը որոշելու համար մարդիկ ստեղծել են սարքեր որոնք կոչվում են ջերմաչափեր:Տարածված են ջերմաչափեր որոնց կառուցվածքում օգտագործված է տաքացման կամ սառեցման ժամանակ մարմինների ծավալների փոփոխվելու երևույթը:

Ջերմաչափեր ստեղծելիս օգտագործվում են հեղուկներ որոնց ծավալի փոփոխությունը կապված է ջերմաստիճանի փոփոխությունից: Օրինակ օգտագործում են հեղուկներ` սնդիկը կամ սպիրտը:Նկարագրենք սնդիկային ջերմաչափի կառուցվածքը: Այն մի ապակյա սնամեջ գունդ է որին զոդված է բարակ, երկար ապակյա խողովակ:Գունդը լցված է սնդիկով և այն տաքանում է հպվելով արտաքին տաք մարմնին: Երբ այն տաքանում է սնդիկը ընդլայնվում է, ընդլայնված ծավալով դուրս են մղվում գնդից միակ հնարավոր ճանապարհով դեպի ապակյա խողովակ, քանի որ վերջինիս ներքին տրամագիծը շատ փոքր է դուրս մղված սնդիկը այս խողովակում ընդունում է երկար սյան տեսք, որի չափը կախված է ջերմաչափի գնդաձև մասի ջերմաստիճանից, չափելով այդ սյան բարձրությունը կարող ենք գնահատել ջերմաչափի գնդաձև մասի ջերմաստիճանը: Սնդիկի սյան բարձրությունը չափելու համար նրա խողովակաձև մասին կցում ենք նրա երկարությունը չափող քանոն` սանդղակ, որի վրա կան հավասարահեռ գծեր: գծերին կարելի է կցել թվեր որոնց տակ մենք կհասկանանք ոչ թե սյան երկարությունը այլ ջերմաստիճանի չափը: խնդիրը կայանում է նրանում թե ինչպես կառուցել ցուցնակը,քանի գիծ լինի և ինչպիսի ձևով նրանց նշանակենք, որպեսզի բոլոր ջերմաչափերի ցուցմունքները միմիանց հետ համընկնեն, այսինքն արտաքին միջավայրի նույն ջերմաստիճանը բոլոր ջերմաչափերով էլ, նրանց սնդիկի սյուներով էլ ցուցեն նույն թիվը: Պրակտիկայում տարածված է ցելսիուսի սանդղակը որի դեպքում գծիկով նշվում է սանդղակի վրա սյան բարձրության այն արժեքը , երբ ջերմաչափին շրջապատող ջուրը դառնում է սառույց, իսկ գծիկին վերագրում են 0 թիվ,գծիկով նշվում է սանդղակի վրա սյան բարձրության այն արժեքը երբ ջուրը տաքացնելով սկսում է եռալ և գծիկի վրա գրում ենք 100:Ապա այդ երկու գծիկների միջև ընկած հեռավորությունը բաժանում են 100 մասի, առաջին գծիկը ներկայացնում է 0 աստիճանն ըստ ցելսուսի, իսկ վերջին գիծ 100 աստիճան ըստ ցելսիուսի, իսկ միջանկյալ 100 գծիկները համապատասխանաբար ներկայացնում են 0-ից 100 տիրույթում ընկած և ամբողջ թվով ներկայացված ջերմաստիճանները: Շարունակելով նույն մաշտաբով գծանշումը 100-ից բարձր 0-ից ցածր տիրույթը ցուցնակի վրա ստանում ենք շատ ավելի մեծ տիրույթ չափող ջերմաչափ: Հարց կառաջանա թե ինչու ենք մենք կապել ջրի սառցակալման և եռման ջերմաստիճանի հետ: Բանը նրանում է որ ջրի սառցակալման և եռման ջերմաստիճանը կախված է ջրի մաքրությունից և այդ ջրին շրջապատող մթնոլորտի ճնշումից, քանի որ այդ ճնշումը ծովի մակերևույթի վրա միշտ նույնն է անկախ իր աշխարհագրական դիրքից իսկ մաքուր ջուր կարելի է ստանալ ջրային գոլորշին սառեցնելու օգնությամբ ապա ստացվում է որ կարելի է ստեղծել նույն ջերմաստիճանը ցույց տվող ջերմաչափ անկախ արտադրողից և արտադրման աշխարհագրական տեղից եթե ջերմաչափի ցուցակավորումը կատարվի վերընշված մեթոդիկայով, բայց միայն ցուցակավորման վայրը պետք է լինի ծովի մակարդակին շատ մոտ վայրում:Սակայն վերընշված ձևով պատրաստված ջերմաչափը ունի թերություններ` նրա ցուցած ջերմաստիճանային տիրույթը համեմատաբար սահմանփակ է,այն հարմար չէ շատ ցածր կամ շատ բարձր ջերմաստիճաններ ցուցելու համար, այդ պատճառով ֆիզիկայում օգտագործվում են շատ ուրիշ ցուցնակներ կամ ջերմաչափի կառուցման ուրիշ սկզբունքներ: Նշենք դրանցից մեկը: Նկատել են, որ, ի տարբերություն հեղուկների, բոլոր նոսր գազերը` ջրածինը, հելիումը, թթվածինը, տաքացնելիս նույն կերպ են ընդարձակվում և ջերմաստիճանի փոփոխման դեպքում հավասարապես են փոփոխում իրենց ճնշումը: Ուստի ֆիզիկայում ռացիոնալ ջերմաստիճանային սանդղակ սահմանելու համար օգտագործում են որոշակի քանակով նոսր գազի ճնշման փոփոխությունը հաստատուն ծավալի դեպքում կամ ծավալի փոփոխությունը հաստատուն ճնշման տակ կախված ջերմաստիճանից:Այսինքն չափելով ճնշման կամ ծավալի փոփոխությունը կարելի է ստանալ նրանց առաջացնող պատճառի ջերմաստիճանի գնահատականը:Այս սկզբունքով կազմված ջերմաստիճանի սանդղակը երբեմն անվանում են ջերմաստիճանների իդեալական գազային սանդղակ:

Ջերմային հավասարակշռություն

2.1-ում նկարագրված սնդիկային ջերմաստիճանի տարածված կիրառումներից մեկն է, երբ այն օգտագործում ենք հիվանդ մարդու մարմնի ջերմաստիճանը չափելու համար:Այդ նպատակով սնդիկային բժշկական ջերմաչափը պահում ենք մարդու թևի տակ 5-8 ր: Նկատում ենք որ այդ ժամանակամիջոցում սնդիկի սյունը, ասյսինք նրա ցուցած ջերմաստիճանը բարձրանում է, ընդ որում սյան` ջերմաստիճանի աճը վերջին 5-8 ր-ներում դանդաղում է, իսկ այնուհետև այդ աճը ի սպառ վերանում է: Ստանում ենք երկարացված սյան որոշակի արժեք, հետևաբար ջերմաչափի հաստատուն ցուցմունք: Եթե մենք ջերմաչափը թևատակում պահենք 8 ր-ից ավել միևնույն է ցուցումը չի փոխվի: Նկատում ենք նաև որ ջերմաչափի գլխիկը, որը իր մեջ պահում է սնդիկի մեծ մասը նույնպես տաքանում է: Ըստ երևույթի նա մարդու մարմնից կլանում է ջերմություն այնքան, որ սնդիկի ջերմաստիճանը դառնում է հավասար մարդու ջերմաստիճանին, ի հաշիվ այդ կլանման սնդիկի ջերմաստիճանը չի կարող ավելի բարձրանալ քան ջերմության աղբյուր հանդիսացող մարդու մարմնի ջերմաստիճանը: Փաստորեն հաստատվում է մարդու մարմնի և սնդիկի միջև ջերմային հավասարակշռություն:Նույնն է տեղի ունենում ցանկացած մարմնի ջերմատիճանը ցանկացած ջերմաչափով չափելիս: Ջերմաչափը մարմնի ջերմաստիճանը երբեք ցույց չի տա անմիջապես նրան հպվելուց հետո: Որոշ ժամանակ է պետք, որպեսզի հավասարվեն փորձարկվող մարմնի և ջերմաչափի ջերմաստիճանները, և նրանց միջև հաստատվի ջերմային հավասարակշռություն, որի ժամանակ ջերմաստիճանը կդադարի փոփոխվել:Եթե միմիանց հպենք երկու տարբեր ջերմաստիճան ունեցող առարկաներ ապա Ժամանակի ընթացքում ջերմային հավասարակշռություն է հաստատվում այդ առարկաների միջև(եթե նույնիսկ այդ երկրորդ առարկան ջերմաչափ չի հանդիսանում),կամ եթե նույնիսկ հպման մեջ ենք մտցնում ոչ պինդ մարմիններ: Դիտարկենք հետևյալ փորձը: Սենյակի ջերմաստիճանի հյութ պարունակող բաժակի մեջ գցենք մի կտոր սառույց, որոշ ժամանակ անց սառույցը տաքանում է և հալչում է, իսկ հյութը սառում է և դառնում հաճելի ըմպելու համար: Փաստորեն սառույցի տեսքով ներկայացված ջուրը մտնում է հյութի կազմի մեջ, իսկ նրա ջերմաստիճանը հավասարվում է ընդհանուր հյութի ջերմաստիճանին: Բազմաթիվ նման դիտարկումների արդյունքում մենք կարող ենք հանգել հետևյալ եզրակացության:Եթե նյութական համակարգում հպման մեջ են գտնվում մարմիններ կամ նյութեր ապա նրանք որոշ ժամանակի ընթացքում նրանց ջերմաստիճանները հավասարվում են այսինքն` անցնում են ջերմային հավասարակշռության վիճակի: Վերընկարագրված ջերմային հավասարակշռության երևույթը նույնպես կարելի է բացատրել մոլեկուլային-կինետիկ տեսության դրույթներով: Միմիանց հպվող մարմիններից տաք մարմնի մոլեկուլների արագությունը (դա ապացուցեցինք 1.1-ում) ավելի մեծ է քան սառը մարմիններինը: Հարվածելով հպվող սառը մարմնի մոլեկուլներին նրանք մեծացնում են այս սառը մոլեկուլների համեմատաբար փոքր արագությունը նրանց հաղորդելով իրենց էներգիայի մի մասը: Բազմաթիվ նման բախումների արդյունքում տեղի է ունենեում նշված մարմինների մոլեկուլների արագությունների հավասարեցում, ջերմային հավասարակշռություն: Իսկ քանի որ բախվող մոլեկուլների միջև կա մեծ հեռավորություն, մոլեկուլները նյութական մասնիկներ են ունեն իներցականություն այդ պատճառով էլ երկու հպվող մարմինների մոլեկուլների արագությունների հավասարեցումը պահանջում է որոշ ժամանակ, որը մենք տեսնում են ջերմափոխանակման ժամանակի տեսքով:

Նյութի մոլեկուլների արագության որոշումը անուղղակի չափումների եղանակով

Այս գլխի առաջին կետում մենք նկարագրեցինք նյութի մոլեկուլների պարամետրերի չափման ռազմավարությունը որը հիմնաված էր անուղղակի չափումների սկզբունքի վրա: Ելնելով սրանից փորձենք ցույց տալ թե ինչպես է մոլեկուլի արագությունը ազդում գազային օբյեկտի չափման համար հարմար այլ պարամետրերի վրա:Ենթադրենք ունենք գազով լցված անոթ: Ըստ մեր մոլեկուլի մասին արդեն ունեցած պատկերացումների նա գտնվում է շարժման մեջ և որոշակի V արագությամբ բախվում է անոթի պատին: Ըստ այս երևույթի պարզեցված մոդելի նրա բախումը պատի հետ առաձգական է: Քանի որ m մասսայով մոլեկուլը V արագությամբ բախվում է պատին հետ է շպրտվում -V արագությամբ: Այս գործընթացում մոլեկուլի սկզբնական և վերջնական շարժման քանակների տարբերությունը (-mv-mv=-2mv) վեր է ածվում անոթի պատի վրա ազդող ուժի իմպուլսի, որի հակազդեցությունը առաջացնում է ճնշում անոթի պատերի վրա: Ըստ մեր պարզեցված մոդելի դիտարկենք մի կողմով պատին հպված l կող ունեցող գազի խորանարդաձև ծավալ: Ենթադրենք այդ խորհանարդում առկա են գազի n հատ մոլեկուլներ: Քանի որ ըստ մեզ այդ մոլեկուլները շարժվում են ամենապատահական ուղություններով ապա խորհանարդի այն նիստի ուղությամբ որ հպված է պատին կշարժվեն մոլեկուլների միայն 1/6 մասը: Հիշենք որ խորանարդը ունի 6 նիստ: Այսպիսով այդ նիստի ուղությամբ անոթի պատի վրա ազդող ուժի գումարային իմպուլսը կլինի հավասար nFt= 2mvn/6(1): որտեղ t-ն այն տևողությունն է որի ժամանակ շարժվող մոլեկուլը ազդում է պատի մոլեկուլի վրա իսկ n-ը դիտարկված խորհանարդում մոլեկուլների քանակն է:Պարզ է t-ն հավասար չէ 0-ի քանի որ գազի մոլեկուլը հետ է շպրտվում պատի մոլեկուլից ոչ թե անմիջական հպման օգնությամբ այլ ի հաշիվ այդ երկու մոլեկուլների շրջապատում գոյություն ունեցող(մոլեկուլի ատոմի միջուկի շուրջը պտտվող էլեկտրոններով պայմանավորված) էլեկտրական դաշտերի փոխազդեցությամբ` հեռաազդեցության շնորհիվ: Ըստ մեր պարզեցրած մոդելի մեր դիտարկած խորհանարդի l կողը համընկնում է հեռաազդեցության չափի հետ: Կատարենք ձևափոխություններ (1)-ի հետ` հավասարման երկու կողմերը բաժանենք l³ վրա: nFt/l³=2mvn/6³: Նշանակենք խորհանարդի ծավալը v'-ով, խորանարդի պատի հետ հպվող մակերեսի չափը S=l² կստանանք nFt/Sl=nmv/3v': Ըստ մեզ հայտնի ճնշում տերմինի սահմանման`այն պատի վրա ազդող գումարային ուժի հարաբերությունը մակերեսին` p=F/s: տեղադրելով հավասարման ձախ մասում կստանանանք p/v=nmv/3v', հետևաբաչ pv'/n=mv²/3: ստացվածը նկարագրում էր վիճակը l չափ ունեցող փոքր խորանարդի համար: փորձենք տալ գործընթացի նկարագիրը ամբողջ անոթի համար հիմնվելով հետևյալ դատողությունների վրա` p ճնշումը խորանարդի պատին նույնն է անոթի ցանկացած մակերեսի վրա: v'/Nհարաբերությունը որը փատորեն ցույց է տալիս մոլեկուլների v' ծավալ ունեցող խորանարդում հաստատւոն է անոթի ցանկացած տիրույթում: Այսինք v'/n=V/N-ի վրա որտեղ մեծ V-ն գազով լցված անոթի ծավալն է, իսկ մեծ N մոլեկուլների քանակն է անոթում: Սրանից կստանանք հետևյալը` pv/N=mv²/3: սակայն գազի մասսան հավասար է նրա բոլոր N-հատ մոլեկուների մասսաների գումարին:Գազի զանգվածը (M) տեղադրելով կստանանք pv/M=v²/3 (3): նկատում ենք որ արտահայտության ձախ մասում գտնվում են մեծություններ որնց կարելի է չափել: Քանի որ V-n անոթի ծավալն է M-ն այդ գազի մասսա, իսկ p-ն ճնշումը: Արտահայտության աջ մասում գտնվում է մոլեկուլի արագության որոնելի արժեքը, որը չենք կարող չափել մոլեկուլի խիստ փոքրության պատճառով:Սակայն այն կարելի հաշվել այս արտահայտության միջոցով` v=3pv'/M(4):

Մոլեկուլի արագության որոշումը նյութի ջերմաստիճանի չափման օգնությամբ

Նախորդ կետում մենք ստացանք (4) բանաձևը որը թույլ է տալիս անուղղակի ձևով` հաշման օգնությամբ որոշել մոլեկուլի արագությունը v-ն: Սակայն դիֆուզիայի և ջերմային հավասարակշռության երևույթի վերլուծության ժամանակ ցույց ենք տվել որ մոլեկուլի արագությունը և ջերմաստիճանն են գտնվում փոխադարձ կապման մեջ: Իսկ (4) բանաձևի աջ մասի բաղադրիչների մեջ չկա ջերմաստիճան: Սա կարող է կասկած հարուցել ընթերցողի մոտ v-ի չափման առաջարկված մեթոդի ճշտության վերաբերյալ:Բայց իզուր, իրոք որ v-ն կախված է նյութի ջերմաստիճանից: Ուղակի (4) բանաձևի p, v, կախված են ջերմաստիճանից: Այնպես որ այդ p և m-ի առկայությունը (4)-ում չի հակասում մեր հիմնական ենթադրությանը: որպեսզի ընթերցողին լինի ավելի համոզիչ ստորև փորձենք դուրս բերել v-ի անմիջական կախվածությունը ջերմաստիճանից:Այդ նպատակով 3-րդ հավասարումը աջ և ձախ մասերը բազմապառկենք 3/2m-ով կստանանք 3pm/2M=mv<sup>2</sup>/2 (5) որտեղ m-ը մոլեկուլի զանգվածն է պարբերական աղյուսակից: Ձախ մասը նշանակենք q-ով: նկատենք որ հավասարման աջ մասը չափելի է: Դիտարկենք հետևյալ փորձը: Վերցնում ենք երեք տքրբեր անոթներում լցված երեք տարբեր գազեր (ջրածին, ազոտ, թթվածին): Այդ երեք անոթները տեղադրենք 0 աստիճան ջրի մեջ:Ջերմային հավասարակշռություն հաստատելուց հետո մանոմետրը չափենք գազի ճնշումները երեք անոթներում և արդեն հայտնի p-ի M-ի` գազի մասսան մեզ հայտնի էր, v-ի որոշվում է անոթի չափերով, m-ը վերցվում է պարբերական աղյուսակից:Հաշվենք q-թիվը բոլոր 3 նյութերի համար: Պարզվում է որ չնայած նյութերը տարբեր էին p,m,v-ն տարբեր էին բայց միևնույն է q-ի հաշվարկային արժեքը ստացվում է նույնը (նշանակենք q_0-ով): Եթե նույն փորձը անենք 50 աստիճանի համար ապա հաշվարկային նոր q-ի արժեքը տարբերվում է 0-ից բայց ստացվում է նորից նույնև անկախ գազի տեսակից: Անոթները ընկղմենք եռացրած ջրի մեջ կստացվի մի նոր q₁ արժեք որը նույնն է բոլոր գազերի համար:ցուցադրենք ստացված արժեքները գրաֆիկական տեսքով: Փորձը ցույց է տալիս որ tga₁=q₁-q₀/t₁-t₀=q₂-q₁/t₂-t₁=tga₁ :tga₂=tga₁ պայմանից բխում է որ q₀,q₁,q₂-ը գտնվում են մի գծի վրա և կախված են միայն ջերմաստիճանից:Այսինքն q-ն գծայնորեն կախված է ջերմաստիճանից ըստ ցելսուսի և կարող է ներկայացնել նյութի ջերմաստիճանը, բայց մեկ այլ սանդղակում: Ըստ գծագրի q=kt+q₀(6):q₀-ն գծային կախումը շեղող թիվն է: Իրոք որ երբ բանաձևի մեջ t=0 ապա q=q₀: Իսկ մենք գրաֆիկով նկատում ենք որ այդ գիծը հատում է կորդինատների առանցքը q₀ կետում: Այսինքն բանաձևը համապատասխանում է գրաֆիկին:Այն փաստը որ q-ն գծայնորեն կախված է t-ից թույլ է տալիս գործածության մեջ մտցնել մի նոր սանդղակ: Այս սանդղակում ջերմաստիճանի արժեքը որոշվում է q-ի արժեքով:Սսկայն (6)-ից երևում է որ այս նոր սանդղակում q-ի մեծությունը հարմար չէ դիտել որպես ջերմաստիճանի արժեքի ցուցիչ: Քանի որ երբ t-ն աճոիմ է 1 աստիճանով ք-ն կաճի k աստիճանով և ամեն անգամ երբ ստիպված լինենք ցելսուսի սանդղակից անցնել այդ նոր սանդղակի ստիպված կլինենք կատարել բազմապատկման և գումարման գործողություն: նշված թերությունը վերացնելու համար բաժանում ենք երկու կողմերը k-ի` q/k=t+q<sub>0</sub>/k նշանակենք q/k-ն T-ով, իսկ q<sub>0</sub>/k-ն t<sub>0</sub> -ով կստանանք T=t+t<sub>0</sub>: Օգտվելով այս արտահայտությունից ֆիզիկայում մտցրել են ջերմաստիճանի չափման նոր ցուցնակ ըստ որի ջերմաստիճանի արժեքը որոշվում է T-ի արժեքով: Այդ նոր սանդղակը կոչվում է բացարձակ սանդղակ:Այս նոր սանդղակում ջերմաստիճանի միավորը կոչվում է Կելվին և նշանակվում է Կ տառով: Արդեն ցելսուսի 1 աստիճանի աճը հավասար է Կելվինի 1 աստիճանի աճին: Քիչ առաջ մենք տեսանք որ q0-ն և k-ն ստացվում են փորձնական չափումների արդյունքում:Հաշվարկները ցույց են տալիս որ t<sub>0</sub>=273 իսկ k գործակիցը որը կոչվում է Բոլցմանի հաստատուն հավասար է 1.38*10<sup>-23</sup>: Մտցնելով ջերմաստիճանի հաշման նոր սանդղակ մենք վերադառնանք մեր սկզբնական նպատակին` այսինքն գտնենք մոլեկուլի արագության և ջերմաստիճանի կախվածությունը: Հիշենք որ 5 հավասարման ձախ մասը մենք նշանակել եին q-ով հետևաբար աջ մասը ևս կարելի է վերցնել հավասար q-ի` q=2/3mv<sup>2</sup>/2(7): Քանի որ ըստ մեր նշանակման T=q/k որից կստանանք mv<sup>2</sup>/2=3kT/2 (8):Այստեղից կստանանք որ v=3kT/m, Վերջինիցս կստանանք v-ի հաշվարկման որոնելի արտահայտությունը: Ստացված բանաձևից կատարենք հետևյալ կարևոր հետևությունները քանի որ E=mv<sup>2</sup>/2 տեղադրելով հավասարման մեջ կստանանք E=3kT/2 այսինքն Կինետիկ էներգիան անմիջական կախվածության մեջ է նյութի բացարձակ ջերմաստիճանից: Այս փոխկապակցութան առկայությունը նկատել ենք դիֆուզիայի երևույթի ուսումնասիրման ժամանակ: Նյութի սառեցումը բերում է նրա մոլեկուլների արադության փոքրացմանը:Քանի որ արագության մոդուլի նվազագույն արժեքը հավասար է 0-ի` այսինքն ատոմները դադարել են շարժվել:Կստանանք որ հավասարման աջ մասը հավասար է 0-ի: Հետևաբար ըստ կելվինի բնության մեջ հնարավոր նվազագույն ջերմաստիճանը ստացվում է երբ T=0:Իսկ T=t+273 բանաձևում T=0 արժեքի դեպքում ստանում ենք որ 0=t_min+273 որտեղից t_min=-273:Այսինքն բնությոան մեջ չի կարող լինել ցելսուսի ավելի ցացր ջերմաստիճան քան -273-ը:

Նյութի մոլեկուլի արագության չափումը մեխանիկական չափման եղանակով

Գազի մոլեկուլների շարժման արագությունը կարելի է չափել նաև մեխանիկական բնույթի փորձով: Փորձը կատարելու համար օգտվենք հետևյալ սարքից: Այն իրենից ներկայացնում է մեկը մեկի մեջ դրված համառանցք գլաններ: Այդ գլանները վերևից և ներքևից փակված են(զոդված են) շրժանաձև թիթեղներով և նրանց միջից օդը հնարավորին չափ հեռացված է: Շրջանաձև թիթեղների կենտրոնով անցնում է արծաթի բարակ շերտով պատված մի ձող որը հանդիսանում է առանցք վերընշված երկու գլանների համար: Առանցքի ներսում տեղադրում ենք հաղորդալար (հատուկ նյութից պատրաստված օրինակ` ոլֆրամ) որի միջով հոսանք թողնելիս հաղորդալարը շիկանում է այն աստիճան որ առանցքի վրա նստեցված արծաթի շերտը հալչում է և ապա գոլորշիանում: Ներքին գլանի պատի վրա բացում են առանցքին զուգահեռ նեղ ճեղք: Երբ շիկացնում ենք հաղորդալարը առանցքային ձողից արծաթի գոլորշու մոլեկուլները դուրս են թռչում և անցնում ճեղքից հետք թողնելով մեծ գլանի ներքին պատի վրա: ապա կատարում ենք նույն փորձը, բայց արտաքինից պտտելով այդ ձողը և ստանալով երկու սինխրոն, նույն անկյունային արագությամբ պտտվող գլաններ: Արդեն այս պայմաններում երբ շիկացնում ենք առանցքով անցնող լարը փորձը ցույց է տալիս որ նման դեպքում մեծ գլանի ներքին մակերևույթին ստացվող շերտը արդեն շեղվում է իր սկզբնական դիրքից գլանների շարժման հակառակ ուղությամբ: Փորձենք բացատրել նկատվող երևույթի պատճառը: Առանցքից պոկվող արծաթի գոլորշու այն մոլեկուլները որոնց հաջողվում է շառավղի ուղությամբ դուրս թռչել ճեղքից իներցիայով շարունակում են շարժվել շառավղի ուղությամբ ներքին գլանից դեպի արտաքին գլանը: Իսկ ինչու շառավղի ուղությամբ: Քանի որ գլաններում չկա օդի մոլեկուլներ որոնք շարժվելով գլանների հետ միասին կհարվածեին ճեղքից դուրս թռչող մոլեկուլներին և կխոտորեին դուրս թռչող մոլեկուլի շարժման ուղությունը հետևաբար այդ մոլեկուլը մնում է իր սկզբնական ուղության մեջ մինչև հասնում է մեծ գլանի ներքին պատին: Բայց քանի որ միջգլանային տարածությունը անցնելու համար նրան պետք է ժամանակ, իսկ այդ ժամանակում մեծ գլանը փոխում է իր դիրքը իներցիայով շարժվող արծաթի գոլորշու մոլեկուլի նկատմամբ, ապա այն արդեն կբախվի արտաքին պատին որոշակի դելտա L շեղումով: Այդ բախման կետերը չեն գտնվի ճեղքի դիմաց:Երբ կրկնում ենք փորձը մեծացնելով գլանի պտտման արագությունները նկատում ենք որ դելտա L շեղումը նույնպես մեծանում է: Պարզ է որ այդ դելտա L-ը կախված է նաև ներքին գլանի ճեղքից դւուրս թռչող մոլեկուլի արագությունից: Այդ արագությունը(v) այստեղ նույնպես ուղղակիորեն չենք կարող չափել, բայց փոխարենը կարող ենք չափել դելտա L-ը որի մեծությունը անմիջապես կախված է v-ից:Եթե ունենանք այդ կախվածության անալիտիկ արտահայտությունը ապա արդեն կարելի է հաշվարկել որոնելի v-ն: Փորձենք գտնել որոնելի f(v) կախվածությունը:Ենթադրենք ճեղքից դուրս թռչող մոլեկուլը երկու գլանների պատերի մեջև ընկած հեռավորությունը անցնում է դելտա t ժամանակամիջոցում: Այսինք t=(R<sub>2</sub>-R<sub>1</sub>)/v որտեղ R<sub>2</sub>-ը մեծ գլանի շառավիղն է, իսկ R<sub>1</sub>-ը փոքր: Այժմ չափումներով հայտնի է նաև գլանների 1վ-ում կատարվող պտույտների քանակը (n), որտեղից T=1/n:Եթե նման մեկ պտույտի ընթացքում (T ժամանակում) արտաքին գլանի ճեղքի դիմացի կետը անցնում է 2ПR<sub>2</sub> տարածություն, ապա ավելի փոքր դելտա t ժամանակամիջոցում այդ կետի պտույտի աղեղը կլինի համեմատական t/T հարաբերությանը, այսինքն դելտա L=t/T*2ПR<sub>2</sub>: տեղադրելով t-ի վերևում ստացված արտահայտությունը կունենանք L=R<sub>2</sub>-R<sub>1</sub>/v*T*(2ПR<sub>1</sub>): տեղադրենք նաև T-ի արժեքը` կունենանք L=(R₂-R₁)*n*2ПR₂/v: որտեղից էլ կստանանք V-ի որոնելի արտահայտությունը:V=(R₂-R₁)*n*2ПR₂/L: Այսպիսով արտահայտության աջ մասի բոլոր պարամետրերը չափելի են և դրա շնորհիվ կարելի է հաշվել v-ի որոնելի արժեքը: Նախորդ պարագրաֆներում մենք ստացել էինք v-ի հաշվարկման տարբեր ձևեր: Փորձից երևում է, որ 1200 ջերմաստիճանում (թելի շիկացման աստիճանը) արծաթի մոլեկուլների մեծամասնության արագությունը գտնվում է 500 մ/վ-ից մինչև 625 մ/վ սահմաններում: Անկարելի է նախատեսել, թե ինչ արագություն և ինչ ուղություն կունենա այս կամ այն մոլեկուլը: բայց ուշագրավ է այն, որ քաոսային շարժում կատարող հսկայական թվով մոլեկուների մեջ գոյություն ունի մի որոշակի բախում ըստ արագության: Պարզվում է, որ գազի տվյալ ծավալում պարփակված մոլեկուլների մեծագույն մասը շարժվում է այնպիսի արագություններով, որոնք մոտ են տվյալ ջերմաստիճանում գազի համար այսպես կոչված ամենահավանական արագությանը: Ստորև զետեղված աղյուսակում բերված է ազոտի մոլեկուլների բաշխումն ըստ արագության` սենյակի ջերմաստիճանում: Աղյուսակից երևում է, որ մոլեկուլների ամենամեծ տոկոսն ունի 300-500 մ/վ արագություն: Մոլեկուների 91%-ի արագությունը գտնվում է 100-700 մ/վ-ի սահմաններում և միայն 9%-ն է, որ 700 մ/վ-ից ավելի և 100 մ/վ -ից պակաս արագություն ունի: Այսպիսով, շատ մեծ թվով պատահական երևույթների մեջ գոյություն ունի որոշ օրինաչափություն: Մի քանի գազերի մոլեկուլների միջին արագությունը 0 ջերմաստիճանի և 760 մմ սնդ. սյան ճնշման պայմաններում. Ջրածին..................1692 մ/վ Ազոտ...................454մ/վ Թթվածին.................425 մ/վ Ջրի գոլորշի............. 566 մ/վ:

Երբ ջերմաստիճանը բարձրանում է, մոլեկուլների արագությունը մեծանում է: Բայց 0-ում ևս այդ արագությունները հսկայական են. նրանք կարող են համեմատվել միայն հրետանային արագության հետ:

Մոլեկուլների ընդհարումների թիվը և ազատ վազքի միջին երկարությունը

Ինչպես տեսանք, սովորական պայմաններում մոլեկուլների շարժման միջին արագությունը չափազանց մեծ է: Մինչդեռ դիֆուզիայի երևույթը ուսումնասիրելիս դիտումները ցույց են տվել, որ նույնիսկ գազերի մեջ, որոնց մոլեկուլներն ամենից ավելի արագաշարժ են, այդ երևույթն ընթանում է համեմատաբար շատ դանդաղ:

Հայտնի է, օրինակ, որ եթե սենյակի մի անկյունում օծանելիք թափենք, ապա օծանելիքի մոլեկուլների դիֆուզիայի հետևանքով հոտի տարածումը համեմատաբար դանդաղ կընթանա` և սենյակի մյուս անկյունում հոտը մենք կզգանք մոտ 10վ անց: Բայց դիֆուզիայի դանդաղ ընթացքը ժխտում է արդյոք այն, ինչ մենք ասել էինք նախորդ պարագրաֆում մոլեկուլների մեծ արագության մասին: Ամենևին ոչ: Բանն այն է, որ մոլեկուլների մեծ քանակի պատճառով օծանելիքի յուրաքանչյուր մոլեկուլը շարժվելիս ճանապարհին հսկայական թվով ընդհարումներ է ունենում ուրիշ մոլեկուլների հետ: Հաշվված է, որ ազոտի յուրաքանչյուր մոլեկուլը` օրինակ, 0°C-ում և մեկ մթն. Ճնշման տակ 1 վրկ-ում մյուս մոլեկուլների հետ ընդհարվում է միջին հաշվով 7,5 միլիարդ անգամ: Այս պատճառով նրա «Ազատ վազքը», այսինքն` այն միջին ճանապարհը, որ նա կատարում է մի ընդհարումից մինչև մյուսը, չափազանց փոքր է: Մենք կարող ենք հաշվել այդ ճանապարհը, եթե մոլեկուլի միջին արագությունը բաժանենք ընդհարումների միջին թվի վրա: Այսպես, օրինակ, ազոտի մոլեկուլի ազատ վազքի միջին երկարությունը հավասար կլինի` λ = 454 * 100/ 7,5 * 10⁹ = 0,000006 սմ: Այսպիսով, սովորական պայմաններում գտնվող գազի մոլեկուլն ավելի շատ «դոփում է մի տեղում», քան առաջ է շարժվում: Նման պատկեր է ստացվում նաև օծանելիքի մոլեկուլների տեղաշարժի ժամանակ և որի պատճառով էլ օծանելիքի մոլեկուլները (չնայած իրենց մեծ արագության) սենյակի մյուս անկյուն են հասնում բավականին ուշացումով: Այսպիսով ամփոփելով վերջին երեք պարագրաֆների նյութը այսուհետև հիմք կընդունենք որ նյութի մոլեկուլները գտնվում են քաոսային, ջերմային շարժման մեջ իսկ մոլեկուլի արագությունը կախված է նյութի ջերմաստիճանից այդ պատճառով էլ մոլեկուլի շարժումը կանվանենք ջերմային-քաոսային շարժում:

Մոլեկուլի չափերի որոշումը

Նյութի մոլեկուլային կառուցվածքի մասին վերջնական պատկերացում կազմելու համար անհրաժեշտ է բացի մոլեկուլի արագությունից իմանալ նաև նրա չափերը: Քննարկենք մոլեկուլների չափերի գնահատման առավել պարզ մեթոդ: Փորձը ցույց է տալիս , որ անհնար է 1մմ³ ծավալով ձիթայուղի կաթիլը ջրի մակերևույթին տարածել այնպես, որ այն զբաղեցնի 0,6 մ²-ուց ավելի մեծ մակերես (նկ.2): Կարելի է ենթադրել, որ ձիթայուղի կաթիլը ջրի մակերևույթին «փռվելիս» առավելագույն մակերես կզբաղեցնի միայն այն դեպքում, երբ նրա թաղանթի հաստությունը կազմված լինի մոլեկուլների մեկ շերտից: Այդ շերտի հաստությունը դժվար չէ որոշել և, հետևաբար, գնահատել ձիթայուղի մոլեկուլի չափերը: Ձիթայուղի շերտի V ծավալը հավասար է նրա S մակերեսի և d հաստության արտադրյալին` V=Sd: Ուրեմն շերտի հաստությունը, հետևաբար, նաև ձիթայուղի մոլեկուլի չափը` d = 0,001 սմ³/6000 սմ² = 1,7 * 10^-7սմ: Այսինքն մոլեկուլը ունի շատ փոքր չափեր: Մոլեկուլների (այդ թվում նաև ձիթայուղի) չափերը մեծ են ատոմների չափերից: Ատոմների տրամագծերը 10^-8 կարգի են: Այդ չափերն այնքան փոքր են, որ անհնար է պատկերացնել: Եթե համեմատակ ատոմի չափը մարդու բռունցքի հետ ապա ստացվում է, որ որքան անգամ բռունցքը փոքր է երկրագնդից այնքան անգամ էլ ատոմը փոքր է բռունցքից:

Իդեալական գազի վիճակի հավասարումը: Գազային օրենքները

Իդեալական գազի վիճակի հավասարումը

Մենք մանրամասն քննարկեցինք իդեալական գազի վարքը մոլեկուլային-կինետիկ տեսությամբ և մասնավորապես մենք ստացանք գազի մոլեկուլի միջին քառակուսային արագության կախվածությունը գազի ճնշումից և ծավալից (տես` ?)և ջերմաստիճանից (տես` /):Սակայն գազի հետ կապված կիրառական խնդիրներ լուծելու ժամանակ յուրաքանչյուր անգամ գազային օբյեկտի հետ կապված վերլուծությունը հասցրել ենք մինչև մոլեկուլային մակարդակ հարմար չէ: Ավելի հեշտ ուղի է երբ գազային օբյեկտի վիճակը բնորոշենք միայն նրա ընդհանուր վիճակը բնորոշող p-ի,v-ի և T-ի միջև: Իսկ կա արդյոք օրինաչափություն, փոխադարձ կախվածություն այս պարամետրերի միջև: Պարզվում է որ այդպիսի օրինաչափություն իրոք գոյություն ունի, դուրս բերենք այդ օրինաչափությունները տեսականորեն և ապա նրանց մենք կհասնենք փորձնական ճանապարհով: Նշվածը հաստատելու համար վերհիշենք ? և ? բանաձևերը:Հարմարության համար v'-ը նշանակված է V-ով:

                       v2=3pV/M
                       v2=3kT/m

Քանի որ հավասարման ձախ մասերը հավասար են կարող ենք գրել որ աջ մասերը նույնպես հավասար են`

                       pV/M=kT/m

Հավասարման աջ մասը բազմապատկենք բաժանենք m'-ի` գազի մոլերի քանակի վրա կստանանք`

                       pV/T=MkTm'/mm':

Քանի որ m'-ը մոլային զանգվածն է իսկփոքր m-ը մեկ մոլեկուլի մասսան է պարզ է որ m'/m-ը կստացվի մեկ մոլ գազում եղած մոլեկուլների քանակը որը բոլոր գազերի համար հաստատուն է, կոչվում է Ավոգադրոյի թիվ: pV/T=MkNa/m': Բոլցմանի k հաստատունի և ավոգադրոյի հաստատունի արտադրյալը անվանում են ունիվերսալ գազային հաստատուն և նշանակում են R տառով: pV/T=M/m'*R: Այսպիսով ստացված հավասարումը տալիս է կապը գազի չափելի պարամետրերի միջև: Եթե փոխում ենք գազի տեսակը նրանով փոխվում է m' մեծությունը: Այս բանաձևից կատարենք հաջորդ հետևությունը: Եթե մենք գազային օբյեկտը սկզբնական վիճակից տաքացման, սեղման օգնությամբ բերում ենք մեկ այլ վիճակի որի բնորոշիչները նշանակենք P₂, V₂, T₂ տառերով ապա քանի որ այդ փորձերի ժամանակ չենք փոխում գազի մասսան կամ նրա տեսակը ապա այս վիճակների համար ճիշտ է հավասարումները p₁v₁/t₁=MR/m', p₂v₂/t₂=RM/m' ապա այդտեղից բխում է որ p₁v₁/T₁=p₂v₂/T₂ Այս հավասարումը կոչվում է Կլապեյրոնի հավասարում, որը ցույց է տալիս որ նոսր գազի հետ կատարվող ցանկացած ֆիզիկական փորձեր որը փոխում է նրա վիճակը և բնական նրա վիճակի պարամետրերը բայց միևնույն է pV/T հարաբերությունը մնում է անփոփոխ: Այս օրինաչափության մեջ կարող ենք համոզվել նաև փորձնական ճանապարհով:

Մարմնի ներքին էներգիա, Ջերմադինամիկա

Մարմնի ներքին էներգիան:

Ելնելով նախորդ գլուխներից մենք արդեն գիտենք, որ մոլեկուլները, որոնցից կազմված են մարմինները, գտնվում են շարժման մեջ:Այս դրույթը ճիշտ է թե գազերի թե հեղուկների և թե պինդ մարմինների համար, այսպես` 1. Գազի մոլեկուլները տարբեր արագություններով և ուղղություններով քաոսային շարժում: 2. Հեղուկների մեջ մոլեկուլները կարող են տեղափոխվել մեկը մյուսի նկատմամբ, ինչպես նաև տատանվել կամ պտտվել: 3. Պինդ մարմինների մեջ մոլեկուլներն ու ատոմները ճոճվում են որոշ միջին դրքերի շուրջը: Քանի որ մոլեկուլները ունեն մասսա և ըստ վերընշվածի միշտ գտնվում են շարժման մեջ ապա նրանք ցանկացած նյութական շարժվող օբյեկտի նման կունենան կինետիկ էներքիա:Նախորդ գլուխներում նշված էր նաև որ մոլեկուլները միմյանց ձգում կամ վանում են կախված նրանց միջև եղած հեռավորությունից` կախված նրանց փոխադարձ դիրքից: Այսինքն եթե մոլեկուլը ինչ որ պահ ընդունենք անշարժ ապա հարևան մոլեկուլի առկայության հաշվին այդ մոլեկուլի կողմից անշարժ մոլեկուլի վրա սկսում է ազդել վանող կամ ձգող ուժեր, որոնց հաշվին նա սկսում է շարժվել: Իսկ նման շարժումը ցույց է տալիս որ նա արդեն օժտված է կինետիկ էներգիայով: Սակայն մենք գիտենք որ էներգիան չի կարող ոչնչից առաջանալ ուրեմն այն եղել է մոլեկուլի մոտ <<թաքնված տեսքով>> և պայմանավորված է եղել իր հարևան մոլեկուլների նկատմամբ ունեցած դիրքով: Իսկ նման էներգիան մենք անվանում ենք պոտենցիալ էներգիա: Այսպիսով ժամանակի ցանկացած պահին մարմնի մոլեկուլը ունի թե կինետիկ և թե պոտենցիալ էներգիա: Նրանք երկուսը միասին կազմում է մոլեկուլի լրիվ էներգիան, իսկ նման մոլեկուլներից կազմված մարմինը կունենա իր բաղադրիչ մասերի` մոլեկուլների էներգիաների գումարը, որը մենք հետագայում կանվանենք մարմնի ներքին էներգիա: Նկատենք որ այս ներքին էներգիան առկա է մարմնի մոտ եթե նա նույնիսկ անշարժ է: Իհարկե եթե մենք մարմինը դնում ենք շարժման մեջ նա ձեռք կբերի որոշակի (արտաքին) մեխանիկական էներգիա,պայմանավորված մարմնի շարժման արագությամբ և մասսայով իսկ նրա լրիվ էներգիան կլինի ներքին էներգիայի և արտաքին մեխանիկական էներգիայի գումարը: Իսկ քանի որ մարմնի ներքին էներգիան բաղկացած է երկու բաղադրիչից, ապա մարմնի էներգետիկ վիճակը կարող ենք բնորոշել հետևյալ հավասարումով` Մարմնի ընդհանուր էներգիա=Մարմնի արտաքին մեխանիկական էներգիա + մարմնի ներքին կինետիկ էներգիա + մարմնի ներքին պոտենցիալ էներգիա: Կատարենք սիմվոլային նշանակումներ` E-Մարմնի ընդհանուր էներգիա, E<sub>1</sub>-Մարմնի արտաքին մեխանիկական էներգիա, E<sub>2</sub>-մարմնի ներքին էներգիան, E'<sub>2</sub>-մարմնի ներքին կինետիկ էներգիա, E2-մարմնի ներքին պոտենցիալ էներգիա: Նման նշանակումների դեպքում մարմնի էներգետիկ վիճակը կարելի է բնորոշել հետևյալ հավասարումով`

                                        E=E1+E2=E1+E'2+E2

Նշենք, որ այս վերջին դուրս բերումը մեզ համար ինքնանպատակ չէր:Մարմինները բնության մեջ մասնակցում են ամենատարբեր ֆիզիկական գործընթացների` մարմինների շփումներ, բախումներ: Մենք կփորձենք բացատրել նրանցում նկատված երևույթները, դիտարկելով նրանց որպես բաղադրիչների արժեքների փոփոխման, կամ նրանց փոխակերպման հետևանք:

Ջերմահաղորդությունը որպես մարմնի ներքին էներգիայի տեղափոխություն, ջերմություն, ջերմության քանակ հպման դեպքում

2-րդ գլխի 3-րդ պարագրաֆում մենք նկարագրել էինք ջերմային հավասարակշռության երևույթը, որը առկա էր երբ տաք մարմինը հպում ենք սառը մարմնին և որոշ ժամանակ անց նկատում ենք նրանց ջերմաստիճանների հավասարեցում: Միմիանց հպվող մարմիններից տաք մարմնի մոլեկուլների արագությունը (դա ապացուցեցինք 1.1-ում) ավելի մեծ է քան սառը մարմիններինը: Հարվածելով հպվող սառը մարմնի մոլեկուլներին նրանք մեծացնում են այս սառը մոլեկուլների համեմատաբար փոքր արագությունը նրանց հաղորդելով իրենց էներգիայի մի մասը: Բազմաթիվ նման բախումների արդյունքում տեղի է ունենեում նշված մարմինների մոլեկուլների արագությունների հավասարեցում: Իսկ քանի որ բախվող մոլեկուլների միջև կա մեծ հեռավորություն, մոլեկուլները նյութական մասնիկներ են ունեն իներցականություն այդ պատճառով էլ երկու հպվող մարմինների մոլեկուլների արագությունների հավասարեցումը պահանջում է որոշ ժամանակ, որը մենք տեսնում են ջերմափոխանակման ժամանակի տեսքով: Այսպիսով ի հաշիվ տաք մարմնի մոլեկուլների արագությունների անկման տեղի է ունենում նրա ներքին կինետիկ էներգիայի անկում կամ փոքրացում, իսկ ի հաշիվ սառը մարմնի մոլեկուլների արագությունների մեծացման տեղի է ունենում նրա ներքին կինետիկ էներգիայի աճ: Փաստորեն տեղի է ունենում տաք մարմնի ներքին էներգիայի մի մասի փոխանցումը սառը մարմնին: Մինչև 18-րդ դարի երկրորդ կեսը ջերմային հավասարակշռության պրոցեսները ուսումնասիրելիս դեռևս չէին օգտվում նյութերի ներքին էներգիանների և նրանց փոխանակման հասկացողություններից, փոխարենը ընդունում էին, որ կա մի անկշիռ մեծություն` ջերմություն, որ տաք մարմնում շատ էր, սառում` քիչ: Իսկ նրանց հպման ժամանակ տեղի է ունենում որոշակի ջերմաքանակի տեղաշարժ տաքից դեպի սառը մարմին: Հետագայում միայն հասկացվեց, որ ջերմություն, ջերմաքանակը դա նույնն է ինչ-որ մարմնի ներքին էներգիան, կամ նրա որոշակի քանակը: Սակայն քանի որ ջերմություն, ջերմաքանակ հասկացողությունները արդեն մտել էին գիտության մեջ այդ պատճառով դրանք չհանվեցին օգտագործումից: Այնպես որ ներքին էներգիաների տեղափոխումը տաք մարմնից դեպի սառը մարմին արդեն իսկ սահմանված տերմիններով անվանեցին ջերմահաղորդություն: Ջերմահաղորդությունը տեղի է ունենում ինչպես մարմինների անմիջական հպման ժամանակ (թեյամանը էլեկտրական սալի վրա), այնպես էլ երբ նրանք իրարից հեռու են գտնվում օրինակ` մարմինների տաքանալն արևից: Տաք մարմնի հեռաազդեցությունը սառը մարմի վրա կատարվում է այսպես կոչված էլեկտրամագնիսական ալիքների օգնությամբ` ունի ավելի բարդ բացատրություն, այս երևույթի ուսումնասիրմանը կանդրադառնանք հետագայում: Ջերմահաղորդության պրոցեսում մարմնի ստացած կամ տված էներգիայի համար որպես չափ ծառայում է մի հատուկ մեծություն, որ կոչվում է ջերմության քանակություն: Որպես ջերմության քանակի միավոր ընդունված է ջերմության այն քանակքը, որ անհրաժեշտ է 1 գ ջուրը 1 աստ տաքացնելու համար: Ջերմության այդ քանակի միավորը կոչվում է կալորիա (կրճատ նշանակումը` կալ): Գործածվում է նաև 1000 անգամ ավելի մեծ միավոր` կիլոկալորիա (կկալ):

Մարմնի ջերմունակությունը որպես ներքին էներգիա կուտակելու և պահպանելու ունակություն

Դիտարկենք հետևյալ փորձը` վերցնենք 1կգ ջուր և գազայրիչով տաքացնենք t<sub>0</sub> աստիճանից մինչև t<sub>1</sub> աստիճան: Ապա այդ նույն գազայրիչով մինչև նույն ջերմաստիճանը տաքացնենք 1կգ պղինձ, կնկատենք որ ջրի տաքացումը տևեց շատ ավելի երկար, այսինքն նա պահանջեց վառելանյութի ավելի մեծ ծախս հետևաբար մենք նրան հաղորդեցինք շատ ավելի մեծ ջերմաքանակ: Եթե մենք այդ երկու մարմինները հեռացնենք գազայրիչից, ապա կնկատենք, որ ջուրը կսառչի և կբերվի սենյակային ջերմաստիճանի շատ ավելի երկար ժամանակամիջոցում քան պղինձը: Այս փորձերում երկու մարմիններն էլ հանդես բերեցին ջերմություն կլանելու պահելու և ապա հետ տալու ունակություն: Սակայն ջրի մոտ այդ ունակությունը քանակապես ավելի մեծ էր, և որպեսզիսի հետագայում կարողանանք մարմինները համեմատել ըստ այդ հատկության ֆիզիկայում մտցվում է մարմնի ջերմունակություն հասկացությունը: Իսկ ինչպես հաշվենք այդ ջերմության արժեքները տարբեր մարմինների համար: Այժմ շարունակենք մեր փորձը` տաքացնենք նույն մարմինները մինչև մի նոր t₂ աստիճան (t₂>t₁): Փորձերը ցույց են տալիս, որ եթե Q₁-ով նշանակենք t₁ աստիճանին հասցնելու համար անհրաժեշտ ջերմության քանակը, իսկ Q₂-ով t₂ աստիճանին հասցնելու համար ջերմության քանակը, նկատում ենք, որ եթե t₂>t₁ ապա ստացվում է Q₂>Q₁: Կրկնելով փորձերը տարբեր t-երի համար, մենք նկատում ենք, որ դրանց հասնելու համար անհրաժեշտ ջերմաքանակները`Q-երը ստացվում են համեմատական այդ t-երի արժեքներին: Նկատված օրինաչափությունը կարելի է ներկայացնել հետևյալ մատեմատիկական արտահայտությամբ Q= C*m*(t-t<sub>0</sub>) այստեղ` t₀-ն մարմնի սկզբնական ջերմաստիճանն է (միջև տաքացնելը): m-ը տաքացվող մարմնի մասսան է, c-ն հաստատուն թիվ Իրոք որ, եթե մեծացնենք աջ մասում t փոփոխական, ապա մեծանում է նաև ձախ մասի Q-ն: Նմանապես եթե նեծացնենք m-ը ապա նույնպես մեծանում է Q-ն: Նկատենք, որ փորձերում եթե մեծացնենք տաքացվող մարմնի մասսան(m),ապա նրան համեմատական մեծանում է նաև նույն t ջերմաստիճանին հասցնելու համար անհրաժեշտ ջերմության քանակը(Q): Այսպիսուվ մեր առաջարկաց բանաձևը լիովին արտահայտում է իրականում փորձերում նկատվող Q-ի կախվածությունը t-ից և m-ից: Միայն թե ջրի դեպքում C ստացվում է ավելի մեծ, քան պղնձի մոտ: Որպեսզի ստանանք c-ի թվային արժեքը և հետագայում այն օգտագործենք ինժեներական հաշվարկներում, վերցնում ենք t-t₀=1°C, իսկ m=1գ, ապա ստանում ենք որ Q=C և այսպիսով C-ն ցույց է տալիս ջերմության այն քանակը, որն անհրաժեշտ է տվյալ մարմինը կազմող նյութի 1գ-ը 1° տաքացնելու համար: Այսինքն C-ն բնորոշվում է տվյալ նյութի ջերմություն կլանելու և պահելու ունակությունը, որը ֆիզիկայում անվանում են տեսակարար ջերմունակություն: Այն հաշվարկելու համար օգտվում ենք վերընշված արտահայտությունից ստացվող հետևյալ բանաձևով C=Q/(m*t-t₀): Արտահայտության աջ մասում տրված փոփոխականները` Q, m, t և t<sub>0</sub> փոփոխականների արժեքները միշտ կարելի է ստանալ փորձի ժամանակ որպես չափվող տվյալներ: Հաշվելով Q-ն ջոուլներով m-ը գրամներով, իսկ t-ն և t<sub>0</sub>-ն կելվիններով, ստանում ենք տեսակարար ջերմունակության արժեքները և հայտնի նյութերի համար նրանց ներկայացնում ֆիզիկական տեղեկատուներում և նրանց օգտագործում ինժեներական հաշվարկներում: Այս տեղեկատուները լայնորեն օգտագործվում են ինժեներական հաշվարկներում: Ստորև բերվում է տեսակարար ջերմունակության արժեքները ներկայացնող մի աղուսյակ տարածված որոշ նյութերի համար: ՈՒնենելով տեսակարար ջերմունակությունը(C), հեշտությամբ կարելի է ստանալ m մասսա ունեցող մարմնի ջերմունակությունը որպես C*m արտադրյալ: Շարադրվածում մենք փաստեցինք, որ նյութերը ունեն ջերմունակություն և այն էլ իրարից խիստ տարբեր: Առաջին հայացքից այդ փաստը անհասկանալի է` օրինակ երբ գազայրիչում այրման արդյունք հանդիսացող շիկացած գազերը շփվում են տաքացող մարմինների հետ ապա տեղի է ունենում ջերմափոխանակում շիկացած գազերից դեպի տաքացող մարմինը, որը ինչպես նկարագրել էինք նախորդ պարագրաֆում առաջանում է երբ շիկացած գազի արագաշարժ մոլեկուլները բախվում էին տաքացող մարմնի մոլեկուլներին: Քանի որ տաքացող մարմինների մոլեկուլների գումարային մասան փորձերում նույնն էին ուրեմն նույն քանակի վառելիք այրելուց պետք է որ երկու մարմինների մոլեկուլները (պղինձ և ջուր) ունենային նույն միջին արագությունները, նույն կինետիկ էներգիան և նույն ջերմաստիճանը (հիշենք` mv²/2=3kT/2): Բայց իրականում դրանք խիստ տարբեր էին նույն վառելիքի քանակի դեպքում ջրի ջերմաստիճանը ավելի քիչ էր աճում սկզբնական վիճակից քան պղնձի ջերմաստիճանը: Փորձենք բացահայտել մեր կատարած <<տրամաբանական>> դատողությունների սխալները: Բանը նրանում է, որ մեր դեպքում ի տարբերություն գազային օբյեկտների ջրի և պղնձի ներքին էներգիան ունի բավականին մեծ բաղադրիչ ներքին պոտենցիալ էներգիայի տեսքով (հիշենք E=E₁+E₂=E₁+E'₂+E₂): Իսկ մարմինները դրսից ստացված էներգիայի հաշվին փոխում են իրենց միջմոլեկուլային կառուցվածը, փոխադարձ դիրքը, իսկ ներքին պոտենցիալ էներգիան հենց պայմանավորված է դրանցով: Այսպիսով մարմնի ստացած ջերմաքանակի միայն մի մասն է վերածվում կինետիկ ներքին էներգիայի, իսկ պոտենցիալ ներքին էներգիայի վերածվող բաղադրիչը էապես տարբեր է ստացվում տարբեր նյութերի մոտ:

Ֆիզիկական երևույթներ որոնք բացատրվում են արտաքին մեխանիկական էներգիան մարմնի ներքին էներգիայի փոխակերպմամբ

Մուրճը տաքանում է հարվածելիս:

Եթե զնդանի վրա դնենք մեխ և նրան ծեծենք մուրճով, քիչ անց նկատում ենք, որ ծեծված մեխը խիստ տաքանում է: Որոշակի չափով տաքանում է նաև ինքը մուրճը: Ըստ մեր մինչ այժմ անցած օրինակների պինդ մարմինը տաքանում էր, ջերմափոխանակության պատճառով, երբ նրան հպվում էր ավելի տաք մարմին: Սակայն մեր նկարագրված փորձում մեխը չէր կարող տաքանալ ջերմափոխանակության պատճառով քանի որ թե զնդանը, թե մեխը, թե մուրճը ունեին նույն ջերմաստիճանը, բայց այնուամենայնիվ մեխը տաքանում է: Փորձենք բացատրել նկատված երևույթը: Մեխին հարվածող մուրճը հարվածի պահին լինում է օժտված որոշակի կինետիկ էներգիայով, պարզ է որ հարվածի պահին մուրճի համընթաց շարժվող մոլեկուլները բախվում են մեխի քաոսային շարժում կատարող մոլեկուլներին, և նրանց հաղորդում լրացուցիչ շարժման քանակ: Արդյունքում մեծանում է մեխի մոլեկուլների շարժման միջին արագությունը, հետևաբար նաև այդ մոլեկուլների կինետիկ էներգիան, և վերջինս համեմատական է մեխի ջերմաստիճանին, որի աճը մենք նկատեցինք մեր փորձում:

Պինդ մարմինը տաքանում է շփվելիս:

Որպես ապացույց հիշենք ինչպես էին մարդիկ նախնադարում ստանում կրակ: Նրանք միմյանց էին շփում երկու չոր փայտիկներ, արդյունքում այդ փայտիկները խիստ տաքանում էին, ջերմություն հաղորդելով իրենց հարևանությամբ գտնվող չոր խոտին, ծխեցնում էին այն: Նրանք փչելով այն, տալիս էին օդի լրացուցիչ հոսք` ստանում կրակ: Իսկ ինչպես բացատրենք այս երևույթը, չէ որ այստեղ ի տարբերություն նախորդ օրինակի չկան հարվածող և հարվածվող պինդ մարմիններ, որոնց դեպքում մենք արդեն բացատրել էինք, ջերմության առաջացման պատճառը: Այս հարցի պատասխանը ստանալու համար առաջարկում ենք խոշորացույցով դիտել մարմիինների շփման մակերևույթները: Կնկատենք մակերևույթի խիստ անհարթություներ, կարծես այդ մակերևույթը մի լեռնաշխարհ է իր լեռնագագաթներով և ձորերով: Պարզ է, որ շփման ժամանակ այդ լեռնագագաթները կբախվեն միմյանց, բախման հետևանքով կտաքանան ինչպես դա կատարվում էր նախորդ օրինակում, երբ մուրճը բախվում էր զնդանին: Որպես համոզիչ օրինակ հիշենք, թե ինջպես ենք այրում լուցկու հատիկը: Նույնիսկ ձեռքով նկատվում է, որ լուցկու տուփի մի նիստը խիստ անհարթ է: Դրա հետ արգորեն շփելով լւցկու հատիկի գագաթը, մենք ստանում ենք բարձր ջերմություն, որից էլ բռնկվում է լուցկու հատիկի գագաթի դյուրավառ ֆոսֆորային գլխիկը:

Օդը տաքանում է մխոցով սեղմելիս:

Ձեր պրակտիայում դուք հաճախ հանդիպել եք իրավիճակի, երբ դուք ձեռքով պոմպի օգնությամբ, օդ ենք մղել հեծանիվի կամ ավտոմեքենայի անվադողի մեջ: Նման դեպքում նկատվում է, պոմպը անվադողին միացնող ռետինե խողովակի տաքացում: Փորձենք բացատրել այդ երևույթը: Ամեն անգամ ուժ ենք գործադրում պոմպի մխոցի վրա, ծախսում էներգիա և տեղաշարժում այդ մխոցը: Շարժվող մխոցը սեղմում է օդը, որի ժամանակ այն հարվածում է սեղմվող օդի մոլեկուլներին: Այդ հարվածներն էլ մեծացնում են հարվածող մոլեկուլների արագությունները, նրանց կինետիկ էներգիան և սեղմվող գազի ներքին էներգիան: Իսկ այս ամենը արտահայտվում է սեղմվող գազի կամ նրան տանող ռետինե խողովակի տաքացման տեսքով: Գազի տաքացում արագ սեղմման դեպքում կամ որ նույնն է արտաքին մեխանիկական էներգիան ներքինի վերածելը կարելի է ցուցադրել նաև հետևյալ փորձով: Վերցնենք կիպ մխոց ունեցող թափանցիկ գլան:Գլանի հատակին դնենք եթերով թրջված բամբակի մի կտոր: Հայտնի է որ արդեն ոչ բարձր ջերմաստիճաններում եթերի գոլորշիները բոցավառվում են(ռեակցիայի մեջ են մտնում օդի մեջ գտնվող թթվածնի հետ): Այժմ արագորեն իջեցնենք մխոցը: Կնկատենք, որ բամբակից դուրս եկող եթերի գոլորշիները բոցավառվում են: Այսինքն մեր կողմից մխոցի վրա կատարված արտաքին աշխատանքը բերեց գլանի միջի գազի ներքին էներգիայի մեծացմանը, այդ գազի ջերմաստիճանի մեծացմանը, որի պատճառով էլ նկատվեց եթերի գլորշիների բռնկում:

Ջերմության մեխանիկական համարժեքը:

ինչպես նկատեցինք մարմնի ներքին էներգիան կարելի է փոխել երկու ճանապարհով` նրան արտաքին մեխանիկական էներգիայի փոխանցման, կամ ջերմահաղորդման ճանապարհով: Մեխանիկական էներգիայի այն քանակը, որ առաջ է բերում մարմնի ներքին էներգիայի նույնպիսի փոփոխություն, ինչպիսին առաջանում է, երբ մարմնին հաղորդում ենք ջերմության քանակի մեկ միավոր, կոչվում է ջերմության մեխանիկական համարժեք: Ջերմության մեխանիկական համարժեքի փորձնական որոշման համար անգլիացի գիտնական Ջոուլը կատարել է հետևյալ փորձը: A կալորիմետրի մեջ ջուր է լցվում: W և W' վայր ընկնող ծանրությունները պտտման մեջ էին դնում K առանցքը` L թիակների հետ: Կալորիմետրն ուներ N միջնորմներ, որոնց նպատակն է մեծացնել շարժական մասերի շփումը ջրի հետ: Ջրի հետ թիակների շփման հետևանքով ջուրը տաքանում էր: Ըստ անկման h բարձրության և ծանրությունների m մասսայի հաշվվում էր կատարված աշխատանքը` A=mgh: Փայտորեն այս մեծությունը դա ծանրոցների պոտենցիալ էներգիան էր սկզբնական դիրքում, որը ծանրոցների վերջնական դիրքում ամբողջովին վեր էր ածվում կինետիկ էներգիայի` արտաքին մեխանիկական էներգիայի, որի հաշվին ոիակները պտտվում էին ջրում: Կալորիմետրի և թիակների ջերմաստիճանի բարձրացման մեծությամբ հաշվվում էր ջերմության այն Q քանակությունը, որ անջատվում էր կալորիմետրի շարժական մասի շփումից ջրի հետ: Այդ մեծությամբ ավելանում էր ջրի ներքին էներգիան: Բազմաթիվ չափումները ցույց տվեցին, որ կատարվող աշխատանքի և Q ջերմության քանակության հարաբերությունը, որով ավելանում էր ջրի ներքին էներգիան, կատարվող աշխատանքի հետևանքով, հանդիսանում է հաստատուն մեծություն: Այդ մեծությունն էլ հանդիսանում է ջերմության մեխանիկական համարժեք: Այդ համարժեքը նշանակվում է I տառով:

                                         I=427կգմ/կկալ=4,1868ջ/կալ

Ջուլը ջուրը փոոխարինեց սնդիկով և նույն արդյունքը ստացավ: Վերջապես, փոխանակ վերցնելու թիակների և ջրի շփման աշխատանքը, Ջուլը կալորիմետրի մեջ ստանում էր երկու մետաղի կտորների շփման աշխատանքը, և ամեն անգամ չափումները նույն մեծությունն էին տալիս ջերմության մեխանիկական համարժեքի համար: Իմանալով ջերմության մեխանիկական համարժեքը, հեշտ է ջերմության քանակի միավորներն արտահայտել աշխատանքի միավորների միջոցով. 1կալ=4,1868ջ կամ 1կկալ=1/860կվտ*ժ:

Ֆիզիկական երևույթներ, որոնք բացատրվում են մարմնի ներքին էներգիան արտաքին մեխանիկական էներգիայի փոխակերպմամբ

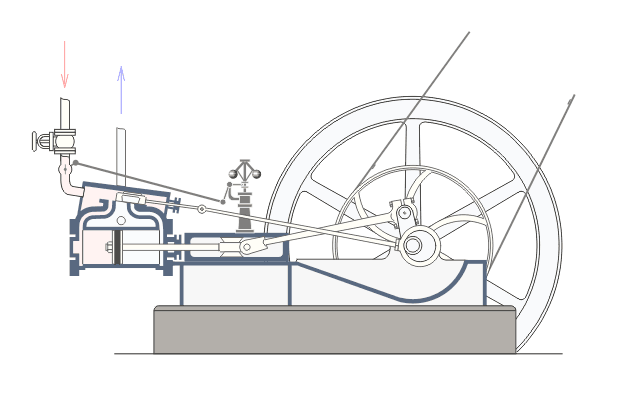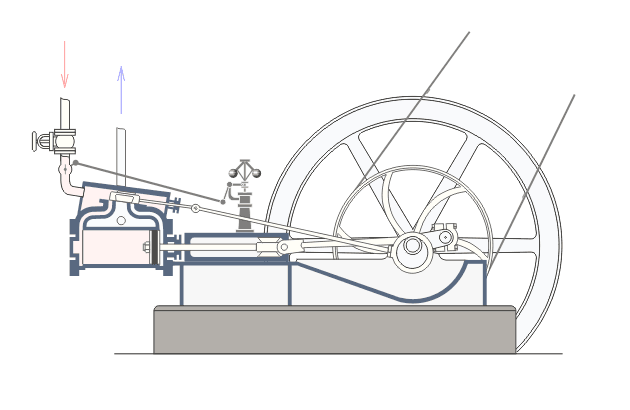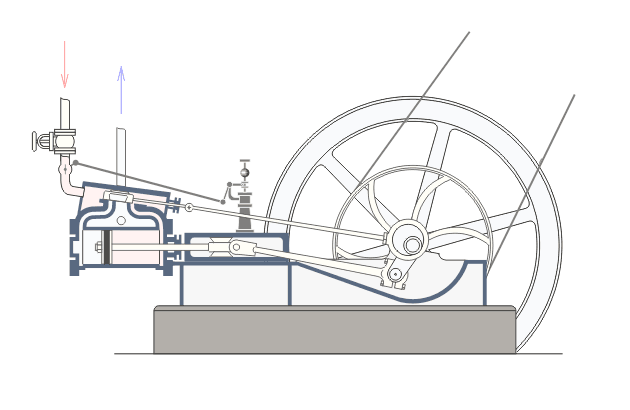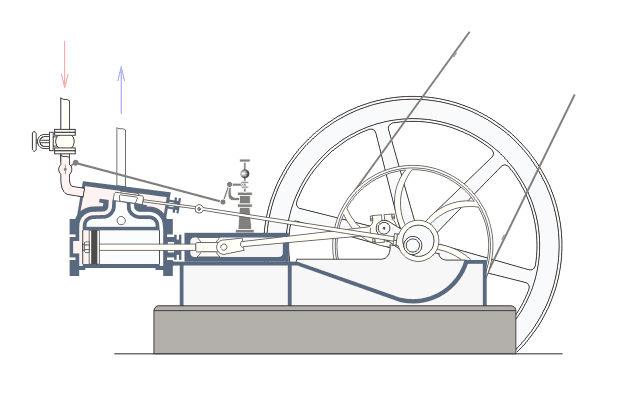
Վերնագրում նշված երևույթները առավել ցայտուն նկատվում են այսպես կոչված ջերմային շարժիչներում: Ջերմային շարժիչ կոչվում է այն մեքենան, որի մեջ վառելանյութի այրումից առաջացող ջերմային էներգիան փոխակերպվում է մեխանիկական էներգիայի: Գոյություն ունեն երկու տեսակի ջերմային շարժիչներ` ներքին այրման շարժիչներ և շոգեշարժիչներ: Նկար ? ում բերված է ջերմային շարժիչի պարզեցված սխեման:Նկարագրենք նրանում ընթացող գործընթացները: : Ստորև`Շոգեշարժիչի սխեման: Գործընթացները շոգեշարժիչում ունեն պարբերական բնույթ: Պարբերության սկզբում բացվում է K₁ փականը(K₂ փակ է) և շոգեկաթսաից տաքացած գոլորշին K₁ փականով մտնում է գլանաձև աշխատանքային խուց: Ըստ երևույթի այդ գոլորշու հոսքի ազդեցության տակ մխոցը խցում կատարում է համընթաց շարժում դեպի աջ: Այդ շարժումը փոխանցվում է շուռտվիկ-սողնակային մեխանիզմին(կազմված էլ1 էլ2 էլ3 էլեմենտներից) , արդյունքում տեղի է ունենում էլ3 էլեմենտի պտույտը առանցքի շուրջ, սակայն այս էլեմենտը կոշտ ամրացված է թափանիվին, այնպես որ մխոցը շարժվելով դեպի աջ` միջև իր հնարավոր աջ վիճակը(պայմանավորված էլ1 էլ2 էլեմենտների գումարային երկարությամբ) ստիպում է պտտվել նաև թափանիվին: Քանի որ թափանիվը ունի մեծ զանգված նա կանգ չի առնում և շարունակվում է իներցիայով պտտվել: Որի ժամանակ նրա հետ ամացված էլ3 էլեմենտը փորձում է հետ մղել մխոցին: Հենց այդ պահին փակվում է K₁ փականը և բացվում է K₂ փականը, որի հետևանքով աշխատանքային խցում առկա գազը այդ փականով դուրս է գալիս դեպի սառնարան: Երբ մխոցը հասնում է առավելագույն ձախ դիրքին, նորից բացվում է K₁ փականը և նորից կրկնվում է նկարագրված գործընթացը : Եթե բաց թողնենք նկարագրված գործընթացի մանրունքները, ապա ստացվում է, որ մենք ջերմություն հաղորդեցինք կաթսային, իսկ արդյունքում ստացանք թափանիվի պտույտը, թափանիվի լիսեռը միացված լինելով գործող սարքերին տեղաշարժում է նրանց և կատարում աշխատանք,այսինքն ստանում ենք արտաքին մեխանիկական էներգիա: Այսինքն կաթսայում տաքացված ջրային գոլորշու ներքին էներգիան վերածվեց արտաքին մեխանիկական էներգիայի:

Ընթերցողի մոտ կառաջանան հարցեր, թե ինչու նկարագրված գործընթացի առաջին փուլում մխոցը որոշակի դժվարությամբ տեղաշարժվում է դեպի աջ: Իսկ ինչու դժվարությամբ, քանի որ նա պետք է կարողանա պտտել մեծ զանգված ունեցող թափանիվը: Ըստ երևույթի նկարագրված գործընթացի երկրորդ փուլում մխոցը հեշտությամբ է տեղաշարժվում դեպի ձախ: Իսկ ինչու հեշտությամբ, քանի որ օգտակար արտաքին մեխանիկական էներգիա ստանալու համար անհրաժեշտ է թափանիվը իր ստացած մեխանիկական էներգիայի(թափի) միայն մի մասը ծախսի մխոցը հետ հրելու վրա: Վերը նշված ինչուներին պատասխանելու համար մանրամասնենք գործընթացները մխոցի ներսում այդ երկու փուլերի ժամանակ:  ..

Որպեսզի վերը նկարագրված առաջին փուլում մխոցը շարժվի դեպի աջ և շարժիչն աշխատանք կատարի անհրաժեշտ է, որ այդ փուլում մխոցում գազի(Ջրային գոլորշի) ճնշումը(P₁) լինի շատ ավելի մեծ, քան մխոցից աջ գտնվող գազի ճնշումը: Ցույց տանք որ մեր նկարագրած սխեմայում p1-ը կարող է մեծանալ: Այս փուլում բաց K₁ փականով աշխատանքային խուց մտնող ջրային գոլորշին տաքացվելով կաթսայում ձեռք է բերել մեծ ներքին էներգիա: Այսինքն մեծանում են այդ գոլորշու մոլեկուլների կինետիկ էներգիան: Մենք արդեն գիտենք, որ այն ներկայացվում է mv²/2 բանաձևով, որտեղ m-մոլեկուլի մասան է, իսկ V-ն նրա արագությունը: Փաստորեն մոլեկուլի կինետիկ էներգիայի մեծացումը բերում է այս V-ի մեծացմանը: Մեծ արագությամբ բախվելով աշխատանքային խցի պատերին և մխոցին, այդ մոլեկուլները, առաջացնում են ճնշում մխոցի վրա, իրենց m-ով և v-ով պայմանավորված շարժման քանակի մի մասը փոխանցում են մխոցին, որի հաշվին մխոցը տեղաշարժվում է դեպի աջ: Այսպիսով շարժվող մխոցի հետ մոլեկուլների առաձգական բախումների դեպքում նրանց կինետիկ էներգիան փոփոխվում է, և նրա հաշվին մենք ստանում ենք մխոցի տեղաշարժով պայմանավորված մեխանիկական էներգիա, որն էլ ձևափոխվում է թափանիվի պտտական շարժման մեխանիկական էներգիայի:

Նկարագրված շոգեմեքենայի հետ կապված ինժեներական հաշվարկներ կատարելու համար անհրաժեշտություն է առաջանում ունենալ կատարված աշխատանքի մեծության կախվածությունը շոգեմեքենայի պարամետրերից: Մենք արդեն նշեցինք, որ մխոցի աջ շարժման ընթացքում որոշակի ուժով(F) գոլորշին ազդում է մխոցի վրա, պարզ է որ այն համեմատական է P ճնշմանը և մխոցի մակերեսին (S) (F=P*S): Գոլորշին ընդարձակվում է և մխոցը տեղաշարժվում է F ուժի կողմը h=h2-h1 փոքր հեռավորությամբ: Եթե տեղափոխությունը փոքր է, ապա գազի ճնշումը այդ ընթացքում կարելի է համարել հաստատուն, հետևեբար նաև հաստատուն կարելի է համարել նաև F-ը: Մխոցը տեղաշարժվելով h չափով կատարում է որոշակի աշխատանք (A): Ելնելով մեզ հայտնի մեխանիկական աշխատանքի սահմանումից (մարմնի կատարած մեխանիկական աշխատանքը համեմատական է մարմնի վրա ազդող ուժի, և այդ մարմնի անցած ճանապարհի արտադրյալին)
                         A=F*(h2-h1)=P*s*(h2-h1)=P(h2*s-h1*s)

V տառով նշանկենք աշխանտանքային խցի ծավալը, որն հավասար՝ V=S*h, կունենանք, որ՝

                         A=P*(V2-V1)=P*(delta)V:

Ստացվածից կարելի է կատարել ինժեներական հետևություն, որ շարժիչի կատարած աշխատանքը (կամ նրա հզորությունը) ուղիղ համեմատական կերպով կախված է խցի ծավալից (այսինքն նրա չափսերից) և նրանում առկա գոլորշու ճնշումից: Սակայն իդեալական գազի հավասարումից մեզ հայտնի է, PV=n*R*T կախվածությունը: Քանի որ մենք ընդունել ենք, որ P-ն հաստատուն է հետևաբար (delta)V-ն կառաջացնի T-ի փոփոխությունը՝ (delta)T, ընդ որում T₂>T₁: Տեղադրելով աշխատանքի բանաձևի մեջ ստանուն ենք, որ A=n*R*(delta)T: Ստացանք որ շարժիչի կատարած աշխատանքը կախված է շարժիչի խցի չափսերից և շոգեմեքենայում օգտագործվող այրիչի տված ջերմաքանակից: Այս կախվածությունը օգտագործվում է ինժեների կողից պահանջվելիք հզորության շարժիչ նախագծելու համար: Նման նախագծման ժամանակ որոշվում է խցի չափսերը և այրիչ տեսակը: